Mehr Lernerfolg – Was Schach und MINT-Fächer miteinander verbindet
„Das Schachspiel ist nicht bloß eine müßige Unterhaltung. Verschiedene schätzbare und im Laufe des menschlichen Lebens nützliche Eigenschaften des Geistes können dadurch erworben oder gekräftigt werden, so dass sie Gewohnheiten werden, die uns nie im Stich lassen.“ (Benjamin Franklin)[1]
Die Stärke der Industrienation Deutschland gründet sich auf das naturwissenschaftliche Know-how und die Ingenieurkunst. Attraktive Berufe mit guten Verdienstmöglichkeiten, zu denen die MINT-Berufe zählen, setzen hinreichend gute mathematische Fähigkeiten und gute Sprachfähigkeiten voraus. Der Fachkräftemangel und die Schaffung von Zukunftsperspektiven gebieten, dass alles unternommen werden muss, um den Schülern das Aneignen mathematischer Kenntnisse und sprachlicher Fertigkeiten zu erleichtern und den Weg zu den MINT-Berufen zu ebnen. Leider bescheinigen verschiedene Studien der letzten Jahre den deutschen Schülern schlechter werdende Kenntnisse und Fähigkeiten in Mathematik. Die Ergebnisse der in 2018 durchgeführten Befragung mit Neuntklässlern, wie sie den Mathematikunterricht einschätzen, geben deutliche Hinweise auf wirksame Maßnahmen zur Leistungsverbesserung:
„Im Rahmen der Studie konnte die theoretisch hergeleitete These, dass der Mathematikunterricht systematisch zur Meidung von Mathematik erzieht, empirisch bestätigt werden. Über Schulen, Bundesländer und Schulformen hinweg bringt der gegenwärtige Mathematikunterricht große Gruppen von Schülern hervor, die sich nicht für Mathematik interessieren und darüber hinaus gelernt haben, die Beschäftigung mit Mathematik mit Unwohlsein zu verbinden. Damit ist die Vermutung gestützt, dass der Mathematikunterricht dazu beiträgt, einen Teil der Schülerschaft zu meidenden Duldern der Mathematik zu erziehen…“[2]
Das altehrwürdige und weltweit verbreitete Schachspiel ist auch im 21. Jahrhundert ein geeignetes Instrument, um die Herausforderungen im Zeitalter von Computer und Künstlicher Intelligenz zu meistern. Weltweite Untersuchungen belegen, dass das Schachspielen zu besseren Schulleistungen führt. Außerdem ist Schach eine kostengünstige Möglichkeit, den Schülern den Zugang zu Mathematik und Naturwissenschaften leichter zu gestalten, weil Schach überall gespielt werden kann und die dafür notwendigen Utensilien nicht teuer sind. Im Schachspiel lernen die Schüler spielerisch unterschiedliche Fähigkeiten, die sich auf die naturwissenschaftlichen Schulfächer und persönliche Einstellungen der Schüler positiv auswirken. In dem vorliegenden Plädoyer für „Schach in der Schule“ werden die im regelmäßigen Schachunterricht liegenden Ressourcen für mehr Lernerfolg beschrieben. Zunächst werden einige Vorbetrachtungen angestellt.
Inhaltsübersicht
1. Mathematik und Deutsch – Fähigkeiten der Schüler in Deutschland
1.1. Ursachen für Probleme in Mathematik und Deutsch
1.2. Angst vor dem Unterrichtsfach Mathematik und den MINT-Fächern
1.3. Welche Fähigkeiten werden in Mathematik und den MINT-Fächern benötigt?
2. Mustererkennung in Schulfächern wie Mathematik, Geometrie, Deutsch
2.1. Mathematik in der Schule – Mustererkennung
2.2. Wahrscheinlichkeitsrechnung – Musterkennung und geistige Vorwegnahme
2.3. Geometrie in der Schule – Musterkennung und Planung
2.4. Sprache und Mustererkennung
3. Probleme bei der Messung des Lernerfolgs
4. Langanhaltende Leistungserfolge beim Lernen durch Schachspielen
5. Schach fördert Inklusion nachhaltig
6. Warum Schach sich positiv auf Mathematik und die MINT-Fächer auswirkt
6.1. Schachspieler denken in Bildern
6.2. Schach fördert die kreative Problemlösung
7. Mit dem lerndidaktischen Spiel „Schach“ kostengünstig zu mehr Lernerfolg in der Schule
Referenzen
Anhang A Übersicht wissenschaftlicher Arbeiten zu Schach in der Schule
Downloads – Beitrag als PDF-Datei, Anhänge A bis C als PDF-Dateien
„Plädoyer für Schach in der Schule“ in Englisch

Wikinger-Schachspiel, Messing- und Kupferblech, Künstler: Andrzej Nowakowski
1. Mathematik und Deutsch – Fähigkeiten der Schüler in Deutschland
Laut dem IQB-Bildungstrend 2021 haben sich bei den Viertklässlern die Kompetenzen in Deutsch und Mathematik deutlich verschlechtert. Der Anteil der Schüler, die in Orthografie den Mindeststandard verfehlen, beträgt für Deutschland insgesamt etwa 30 Prozent. Der Anteil der Viertklässler, die in Deutschland insgesamt den Regelstandard im Bereich Orthografie erreichen oder übertreffen, beträgt etwa 44 Prozent, also weniger als die Hälfte.[3]
Der Anteil der Viertklässler, die im Kompetenzbereich Lesen mindestens den Regelstandard erreicht haben, sank auf 58 Prozent im Jahr 2021.[4] Das ist mehr als bedenklich, schließlich wird für das Lösen der Textaufgaben in Mathematik, Chemie, Physik, Biologie und Geografie die Kompetenz „Verstehendes Lesen“ benötigt.
Der Anteil der leistungsstarken Schüler, die den Regelstandard erreichen oder übertreffen, hat in den Fächern Deutsch und Mathematik abgenommen. Zugleich hat der Anteil der Schüler, die den Mindeststandard nicht erreichen und damit ein hohes Risiko für einen weniger erfolgreichen Bildungsweg aufweisen, in allen Kompetenzbereichen teils deutlich zugenommen.[5]
Wie sieht es in höheren Klassen aus? Laut der letzten PISA-Studie aus 2018 sank die mittlere mathematische Kompetenz der Fünfzehnjährigen in Deutschland gegenüber PISA 2015 und PISA 2012. Im Vergleich zu dem bei PISA 2012 erreichten Höchstwert ergibt sich bei PISA 2018 ein signifikanter Rückgang der mathematischen Kompetenz. Weiterhin wird festgestellt, dass seit PISA 2003 die Mittelwerte der mathematischen Kompetenz an Gymnasien fast kontinuierlich geringer werden. In PISA 2015 erreichten die Schüler an Gymnasien bereits schwächere Leistungen als in den Erhebungen früherer PISA-Studien.[6]
Insbesondere ist der Anteil der Schüler an nicht gymnasialen Schulen, die nur die untersten Kompetenzstufen erreichen, mit knapp 30 Prozent sehr hoch. Diese haben ein besonders hohes Risiko, die Schule ohne Haupt- oder Realabschluss abzubrechen.
Während die mathematische Kompetenz bei Mädchen in Deutschland laut PISA-Studie 2018 im Vergleich zu PISA 2012 weitgehend unverändert blieb, hat diese bei den Jungen seit 2012 um knapp 17 Punkte signifikant abgenommen.[7]
Die Quote der Jugendlichen mit Abitur oder Fachhochschulreife ist seit 2014 gesunken. Dagegen stieg im selben Zeitraum die Zahl der Schulabgänger, die nicht mindestens einen Hauptschulabschluss erreicht haben. (Spiegel, 23.06.2020)[8]
2019 wurde ein bemerkenswerter Brief an die Kultusministerkonferenz geschrieben, der von hunderten Professoren, Wissenschaftlern und Persönlichkeiten unterzeichnet war. In dem Schreiben wurde beklagt, dass seit dem Brandbrief von hunderten Professoren aus 2017 sich im Lehrplan „Mathematik“ kaum etwas positiv verändert hat.[9] Die Aktualität des genannten Brandbriefes kann am Beispiel der Prozentrechnung illustriert werden. Es gibt Mathematikdidaktiker die beim Lösungsschema Dreisatz (s. Abb.1) wenig Raum für Kopfrechenstrategien sehen.
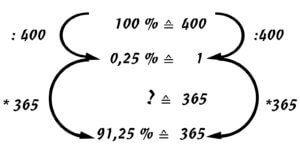
Abb.1 Rechenschema Dreisatz
Aus einer Längsschnittuntersuchung zur Prozentrechnung im Mathematikunterricht weiß man, dass Lernende aller Schularten flächendeckend zwar relativ viele Aufgaben bearbeiten, dabei jedoch flächendeckend weniger als 50 % richtige Lösungen erzielen.[10] In sehr vielen Schulen wird zur Lösung von Prozentaufgaben das Rechenschema „Dreisatz“ gelehrt. Die Zuordnung zu den Begriffen Grundwert, Proportionalitätsfaktor bereitet Schwierigkeiten. Ein Wechsel vom Lösungsschema „Dreisatz“ zum Lösungsschema „Verhältnisgleichung“ scheint vorerst nicht möglich zu sein. Das Lösungsmuster „Verhältnisgleichung als Bruchgleichung“ findet bei Didaktikern wenig Anklang.[11] Nach Auffassung des Verfassers dieses Artikels hat der Dreisatz viele Nachteile hinsichtlich Lernverständnis und Anwendung in anderen Fächern. (siehe Anhang B)
Wir leben heute in einer Informationsgesellschaft, die die Menschen ständig fordert, sich immer wieder mit neuen Wissen und Technologien zu beschäftigen. Die Bewältigung gelingt denjenigen besser, der die dafür erforderlichen Persönlichkeitsmerkmale und Fähigkeiten mitbringt wie Lernbereitschaft, Motivation, Verantwortungsbewusstsein, Zuverlässigkeit, Flexibilität, Gewissenhaftigkeit, Selbstbewusstsein, Offenheit, Aufmerksamkeit, Konzentrationsfähigkeit. Die Wirtschaft befindet sich im globalen Wettbewerb um gut ausgebildete Fachkräfte. Bei den Entscheidungen über Investitionen in neue Standorte oder Erweiterungen bestehender Standorte spielt auch das Vorhandensein qualifizierter Fachkräfte eine Rolle.

1.1. Ursachen für Probleme in Mathematik und Deutsch
Die Nutzung von Zeitungen und Zeitschriften veränderten sich in den letzten Jahrzehnten stark. Im 19. und 20. Jahrhundert boten Zeitungen und Zeitschriften allerlei anspruchsvolle Rätselaufgaben zur Unterhaltung an. Rösselsprungaufgaben in kleinen und großen Feldern, Schach- und Dameaufgaben, Detektivaufgaben, Sprachspiele.

Abb.2 Rätsel aus der Zeitschrift Gartenlaube, 1890[12]
Solche anspruchsvollen Denksporträtsel findet man in heutigen Zeitschriften und Zeitungen selten. Im Internet muss man bewusst solche Angebote suchen und Websites ansteuern bzw. geeignete Apps im Appstore finden und herunterladen. Das zufällige Beschäftigen mit solchen Rätseln und das beiläufige Lernen durch das Lösen solcher Rätsel ist heute schwieriger.
„Wenn Kinder mit Mathematik auf Kriegsfuß stehen, attestieren ihnen Experten häufig eine so genannte Rechenschwäche. Doch dieser Begriff lädt die Schuld zu Unrecht bei den Betroffenen selbst ab, meint der Mathematikdidaktiker Wolfram Meyerhöfer von der Universität Paderborn. Jedes Kind könne rechnen lernen – mit den richtigen Methoden.“[13]
Schüler mit besonderen Schwierigkeiten beim Mathematiklernen in der Grundschule haben Schwierigkeiten sich vom zählenden Rechnen zu lösen und zum denkenden Rechnen überzugehen. Zählendes Rechnen nimmt mehr Ressourcen im Gehirn in Anspruch, dauert länger und stößt bei Rechnen mit größeren Zahlen an Grenzen. Es wird immer schwieriger, Lernfortschritte zu erzielen. Als Prävention werden Übungen zum Zerlegen, Vergleichen, Quantifizieren von Mengen genannt. Die erfolgreiche Prävention stützt sich auf die Fähigkeit des Identifizierens und Benennens von Strukturen und Mengen, die der Lernende haben oder erwerben muss. Viele Schüler haben Probleme mit mehrstelligen Zahlen, dass sie die mehrstelligen Zahlen als Ziffernfolge wahrnehmen und weniger das Zahlenmuster erkennen[14], zum Beispiel, dass zweistellige Zahlen aus den Zehnern und Einer oder die dreistelligen Zahlen aus Hundertern, Zehnern und Einern gebildet werden.
Das Rechnen scheitert – „wenn die Zahlzerlegungen bis inklusive der Zehn nicht vollständig automatisiert wurden und bereits automatisierte Aufgaben nicht für Ableitungen [Mustervergleiche] genutzt werden können, bleibt den Schülern ausschließlich das Zählen als einzig verfügbares Lösungswerkzeug, neben dem Abruf bereits automatisierter Rechenaufgaben. Die Automatisierung ihrerseits wird aber durch die dauerhafte Praxis des zählenden Rechnens zumindest erschwert.“[15] Die geforderte Automatisierung setzt ihrerseits voraus, dass die erforderlichen Informationen in Mustern und Bildern, die untereinander in Beziehung stehen, in einer Bibliothek im Langzeitgedächtnis abrufbereit vorhanden sind. Der wesentliche Vorteil der Automatisierung ist, dass automatische Prozesse parallel ablaufen können, ressourcenschonend sind, keine nennenswerte Aufmerksamkeit und Konzentration benötigen. Das Arbeitsgedächtnis ist das Nadelöhr zum Langzeitgedächtnis. Die eingehenden Informationen im Gehirn werden im Arbeitsgedächtnis verarbeitet, d.h. die Informationen werden identifiziert, verglichen, bewertet, kodiert, gespeichert. Die Ausprägung des Arbeitsgedächtnisses bestimmt dessen Leistungsfähigkeit. Ein unzureichend entwickeltes Arbeitsgedächtnis behindert die Informationsaufnahme und –verarbeitung, was sich negativ auf die Lernleistung auswirkt.
„Geht es im Mathematikunterricht zum Beispiel um den Aufbau von mentalen Vorstellungsbildern, wie dem des 20er-Feldes, muss davon ausgegangen werden, dass Kinder mit besseren Arbeitsgedächtnisressourcen einen Vorteil beim Wissensaufbau haben. Somit erscheint eine Kompensation von defizitären Arbeitsgedächtnisfunktionen zur Schaffung besserer Lernvoraussetzungen notwendig.“[16] Die Addition mehrstelliger Zahlen geht mit einer komplexen Informationsverarbeitung im Arbeitsgedächtnis einher: Das Arbeitsgedächtnis speichert bei mehrstelligen mentalen Additionsaufgaben nicht nur die Summanden und ruft das Ergebnis aus dem Langzeitgedächtnis ab, sondern hält auch Zwischenergebnisse bereit und initiiert und überwacht die Auswahl und Durchführung von komplexen Rechenalgorithmen.[17]
Insbesondere die grammatikalischen Fähigkeiten beeinflussen langfristig das mathematische Lernen.[18] Grammatik enthält das Regelwerk der Sprache und beschreibt die Struktur der Sprache. Die Satzstruktur hat einen Einfluss darauf, welche zusätzliche Information wahrgenommen wird. So kann die Reihenfolge einzelner Wörter den Informationswert einzelner damit bezeichneter Objekte erhöhen oder mindern. Noch schwieriger ist die Vermittlung der phonetischen Information, denn die besondere Betonung eines Wortes kann zu unterschiedlichen Wahrnehmungen der Information führen, beispielsweise, dass zum Handeln aufgefordert wird oder dass ein Vorwurf herausgelesen wird. Daraus lässt sich schlussfolgern, dass ein Minimum an fachlichem Sprachwortschatz vorhanden sein muss, um die über die Sprache erhaltene Information entsprechend ihrer tatsächlichen Absicht aufzunehmen und zu verarbeiten, also zu erkennen, zu vergleichen, zuzuordnen und zu bewerten. Je größer der Sprachwortschatz ist, umso besser ist Kommunikation möglich, weil Sachverhalte besser erfasst, verstanden und reflektiert werden, was bezogen auf die MINT-Fächer von großer Bedeutung ist.
Das Fach Physik wird von Schülern als besonders schwer eingeschätzt. Physikalische Prozesse werden mit der Sprache der Mathematik beschrieben. Die sprachliche Beschreibung des physikalischen Vorganges kann die zugrundeliegenden Mechanismen und Erkenntnisse nicht in der Komplexität und Vielfalt abbilden wie es die dazugehörigen physikalischen Formeln in mathematischer Schreibweise vermögen. Die gefundenen mathematischen Gleichungen sind selbst Teil des Erkenntnisprozesses. In der Atomphysik gibt es viele Beispiele für Vorhersagen von Teilchen, deren Existenz erst viel später durch extrem aufwendige Experimente bestätigt wurden. Die Reduktion realer Prozesse auf mathematische Symbole und Gleichungen bereitet den Lernenden Schwierigkeiten Für das Verständnis und den Lernerfolg im Fach Physik wie auch in anderen Naturwissenschaften und in vielen Bereichen der Betriebswirtschaftslehre kommt es auf die Fähigkeit an, die mathematische Gleichung zu interpretieren, also weitere Erkenntnisse aus der Gleichung abzuleiten.
Beispiel: Geschwindigkeit
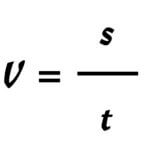
Abb.3 v – Geschwindigkeit, s – Weg, t – Zeit
Die Geschwindigkeit ist der innerhalb einer bestimmten Zeit zurückgelegte Weg. Die Gleichung enthält noch viel mehr Informationen als den gerade genannten Fakt. Die ihr inne liegende Dynamik wird mit der Interpretation sichtbar. Je größer der zurückgelegte Weg in der gleichen Zeiteinheit ist, umso größer ist die Geschwindigkeit oder je weniger Weg in der gleichen Zeiteinheit zurückgelegt wird, umso kleiner ist die Geschwindigkeit. Man kann aber auch herauslesen, dass bei gleicher Geschwindigkeit der zurückgelegte Weg zunimmt, wenn die Zeitdauer wächst. In der Alltagssprache würde man sagen: „Je länger gefahren wird, umso mehr Wegstrecke wird zurückgelegt.“ Nach Umstellung der Formel, kann diese Beziehung unmittelbar abgelesen werden:
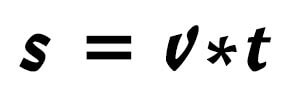
Abb.4
Die Alltagserfahrung ist in der Gleichung enthalten. Die Interpretation der Ergebnisse erfordert Übung, denn die mathematischen Ergebnisse müssen in die reale Welt übersetzt werden. Der Begriff „Leistung“ kommt in der Physik wie in der Betriebswirtschaftslehre vor und ist gleich definiert als „Leistung gleich Arbeit je Zeiteinheit“
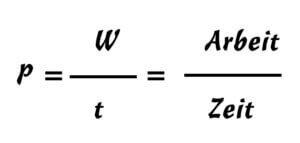
Abb.5 Leistung
Den Unterschied macht die Interpretation des Begriffes „Arbeit“. In der Physik ist Arbeit eine Energiegröße während in der Betriebswirtschaft der mengenmäßige Output gemeint ist.
Der in Deutschland an vielen Stellen anzutreffende Trend der leichten Sprache muss ernsthaft hinterfragt werden. Wortschatzübungen wie Wortfelder verdeutlichen, dass die Sprache ein mächtiges Instrument zur Beschreibung der Wirklichkeit ist. Gute Ausdrucksfähigkeit baut auf einen reichhaltigen Wortschatz auf. Treffende Wortwahl verbessert die Ausdruckskraft und reduziert Missverständnisse in der Kommunikation. Die Fachsprache spiegelt die Gedankenwelt des jeweiligen Faches wieder und normiert die Begriffe der Alltagssprache auf das betreffende Fachgebiet. Ein weiterer Schlüsselfaktor für die geistige und psychomotorische Entwicklung des Kindes ist die Erweiterung des Wortschatzes, denn Kinder brauchen neue Informationen, um einen Gedankenfilter zu entwickeln, der eine Auswahl ermöglicht.[19] Es scheint ein Irrtum vorzuliegen, das „leichte Sprache“ tatsächlich einfacher zu verstehen ist:
„Mit ihren Aussagen im Reflexionsinterview bestätigten die Schüler […] nur teilweise die Annahme, dass Fachbegriffe ein physikalisches Problem verkomplizieren. Tatsächlich wirkt eine Aufgabe mit Fachwörtern und neuen Begriffen auf sie nur auf den ersten Blick schwierig. Bei genauerem Hinsehen erweisen sich die Fachbegriffe dagegen als hilfreich für die Formelfindung, da ohne die Fachbegriffe Bekanntes aus dem Unterricht und Wesentliches für die Bearbeitung fehle.“[20]
1.2. Angst vor dem Unterrichtsfach Mathematik und den MINT-Fächern
„Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.“ (Richard Feynman)[21]
Aus dem Sport und der Medizin weiß man, dass Selbstvertrauen und Willen mächtige Erfolgsfaktoren sind. Angst hingegen fordert den Misserfolg geradezu heraus. So wundert es nicht, dass für die Berufsfindung die Erfolgserwartungen, die man sich in dem jeweiligen Berufsfeld zuschreibt, eine große Rolle spielen. Das Vertrauen in die eigenen Fähigkeiten beeinflusst auch, wie viel Energie für das Erlernen neuer Kompetenzen aufgewendet wird. Die Einstellung, dass man grundsätzlich gut in einem bestimmten Bereich – wie zum Beispiel Mathematik – ist, führt auch zu einer größeren Bereitschaft, mehr Zeit in das Bearbeiten neuer Problemstellungen zu investieren, weil man ex-ante davon ausgeht, dass es einem gelingen wird, die Problemstellung zu lösen (Lin-Siegler et al., 2016).
Persönliche Einstellungen und Überzeugungen haben einen großen Einfluss auf den Lernerfolg, Der Glaube und die Überzeugung der Schüler, dass der Erfolg in den Naturwissenschaften von besonderen Begabungen abhängt, wirkt sich negativ auf ihre Lernmotivation aus. Es hat sich gezeigt, dass solche Überzeugungen Gründe sind, weshalb Schüler naturwissenschaftliche und mathematische Fächer weniger mögen.[22]
Das Berichten darüber, dass auch erfolgreiche Wissenschaftler vor ihren Entdeckungen Misserfolge erlebten, kann den Schülern helfen, ihre Schwierigkeiten im naturwissenschaftlichen Unterricht als normale Ereignisse wahrzunehmen und nicht als Ausdruck mangelnder Intelligenz oder Begabung für diese Fächer. Als erfolgversprechender Weg, die Schüler für Naturwissenschaften stärker zu interessieren, erwies sich, den Schüler zu zeigen, welche Schwierigkeiten Wissenschaftler auf Ihrem Weg zu den Entdeckungen überwinden mussten.[23] Auf diese Weise erfahren die Schüler, dass Fleiß und Beharrlichkeit sich am Ende auszahlen. Kontraproduktiv sind die vielen Äußerungen von prominenten Persönlichkeiten in den Medien, die sich darin übertreffen, zu erklären, wie schwer Mathematik ist. Es muss ein gesellschaftlicher Wandel stattfinden:
„Es geht auch darum, das Image von Mathe in der Gesellschaft zu verbessern, um mehr Heranwachsende für das Fach begeistern zu können. Doch oft sei es laut Professor Weitz noch so, dass es ein kulturelles, gesellschaftliches Phänomen gibt, in dem von vornherein allen implizit klargemacht wird, dass Mathe doof ist. Diese Denkweise hemme das Lernen.“
(Edmund Weitz, Professor für Mathematik und Informatik an der Hochschule für Angewandte Wissenschaften Hamburg,)[24]
Aus Erfahrung weiß man, dass Angst lähmend wirkt. Angst vor Mathematik ist ein ernstzunehmendes Hindernis auf dem Weg zu besseren mathematischen Fähigkeiten.
„Mathematikangst ist eine leistungsbezogene Emotion, die ein Gefühl von Anspannung, Besorgnis oder Furcht bei der Bearbeitung mathematischer Probleme im täglichen Leben und in der Schule beschreibt. Mathematikangst weist negative Zusammenhänge mit der Mathematikkompetenz und dem mathematischen Selbstkonzept auf und trägt dazu bei, dass Situationen vermieden werden, die mathematische Anforderungen beinhalten (z.B. Studiengangs- oder Berufswahl mit mathematischen Inhalten; Pekrun, 2006).“[25]
Die Studie „IQB-Bildungstrends 2021“ erfasste auch die Ängstlichkeit der Schüler. Fast jedes vierte Kind (23%) gab hohe Ängstlichkeit für das Fach Mathematik an. Weniger als die Hälfte der Kinder (40%) gab an, wenig Angst im Fach Mathematik zu haben. Mathematikängstlichkeit bedeutet oft, dass mathematisch anspruchsvollere Berufe vermieden werden, die vielfach bessere Verdienstmöglichkeiten bieten als „nichtmathematische“ Berufe.
Die Zahl der Schüler, die Angst vor Mathematik haben, ist in der Vergangenheit in Deutschland angestiegen. Vor dem Hintergrund des Fachkräftemangels sollte alles getan werden, diesen Trend schnellstens umzukehren.
Wie kann der Mathematikunterricht erfolgversprechender gestaltet werden? Erfolgreiche Lehr-Lernprozesse hängen kaum mit einer bestimmten methodischen Unterrichtsgestaltung beziehungsweise Sichtstruktur zusammen, sondern die Tiefenstrukturen sind entscheidend, die sich auf die Qualität der Auseinandersetzung der Lernenden mit den Lerninhalten und die Interaktionen der Schüler untereinander sowie mit der Lehrkraft beziehen.“ [26]
Unter Tiefenstrukturen sind die psychologisch-pädagogischen Prozessqualitäten von Unterricht zu verstehen, wie beispielsweise kognitive Aktivierung, adaptive Lernunterstützung oder Verstehensklarheit. Tiefenstrukturen können mit drei Unterrichtsqualitätsdimensionen bewertet werden:
- Classroom-Management. Darunter fällt die Klassenführung. Es geht darum, dass die Schüler die Lernzeit effektiv nutzen können, indem die Lehrperson beispielsweise Störungen vorbeugt und für klar strukturierte Abläufe im Unterricht sorgt.
- Konstruktive Lernunterstützung. Dazu gehören Aspekte wie Feedback, Lernprozessunterstützung, Fehlerkultur – also um die Frage, ob Fehler auch als Lernchance gesehen werden.
- Kognitive Aktivierung. Im Zentrum steht hier, ob gute Aufgaben gestellt werden, die differenzieren, anregend sind und auf verschiedenen Kompetenzstufen gelöst werden können.[27]
Einfache Lösungen gibt es nicht. Ein möglicher Weg kann das spielerische Moment im Unterricht sein, bei dem gleichzeitig viele wichtige Kompetenzen gefördert werden. Schach ist ein solches Spiel, das Aktivitäten beinhaltet, die Kindern freudige Spielerfahrungen bieten und gleichzeitig ihr Interesse an der Erforschung der Symbole und Regeln wecken können. Es ist ein Spiel mit weitreichender, universeller Popularität und einem leicht erkennbaren Konzept und Grundregeln.[28]
Das Schachspiel hat seine Qualitäten hinsichtlich der Verbesserung der mathematischen Leistungen von Schülern in vielen internationalen Studien bewiesen. Was sind die Gründe, dass Schach sichtbare Verbesserungen in den schulischen Leistungen, vor allem Mathematik, bewirkt?
1.3. Welche Fähigkeiten werden in Mathematik und den MINT-Fächern benötigt?
„Was Menschen mit der Sprache der Mathematik bezwecken, ist die Beschreibung von Mustern.“ (Lynn Arthur Steen, 1990)[29]
Zur Beantwortung dieser Frage wird die Denk- und Vorgehensweise der Naturwissenschaftler betrachtet. Wissenschaftliches Denken wird definiert als die Fähigkeit, Hypothesen, Theorien und Daten zu generieren, zu testen, zu bewerten und diesen Prozess zu reflektieren.[30]
Mathematik wird als die Wissenschaft von Mustern verstanden. Muster werden oft durch Beziehungen und Funktionen ausgedrückt. Tabellen, Diagramme, Formeln und Grafiken gehören zu den vielen Mitteln, die verwendet werden, um Muster und Beziehungen darzustellen (z. B. zwischen Celsius und Kelvin, Zoll und Zentimeter, Geschwindigkeit und Zeit). Zusammenhänge stellen Querverbindungen her und verdeutlichen Abhängigkeiten; sie zeigen Korrelationen auf oder bestätigen die Eigenständigkeit. Manche Zusammenhänge sind direkt, andere indirekt; manche zeigen stetige Verläufe, andere schwanken; manche sind stetig, andere unstetig. Die meisten können in verschiedenen Darstellungsformen wiedergegeben werden – grafisch, verbal, numerisch oder analytisch. In der Tat werden die Muster der Mathematik oft am effektivsten durch das Zusammenspiel dieser verschiedenen Darstellungsformen sichtbar.[31] Zusammengefasst gründet sich das Lösen mathematischer Aufgabenstellungen auf das Wissen und die Anwendung verschiedener Techniken und Methoden der Mustererkennung.[32]
In Chemie und Physik werden Denkmodelle verwendet, die die Wirklichkeit auf wesentliche Inhalte reduziert und idealisiert. Sachverhalte und Prozesse werden mit mathematischen Symbolen und Gleichungen abgebildet. Im Zuge des Erkenntnisgewinns werden die Denkmodelle erweitert und angepasst. Mathematische Methoden sind erforderlich, um Zusammenhänge zu erfassen, Naturvorgänge zu beschreiben, Lösungen zu finden und Ergebnisse zu überprüfen.
Sach- bzw. Textaufgaben in den naturwissenschaftlichen Fächern spiegeln gewöhnlich real mögliche Ereignisse wieder. Ziel der Textaufgaben ist es, Praxisnähe zu erreichen und die Schüler zur Anwendung mathematischer und naturwissenschaftlicher Methoden zu befähigen. Der Weg zur Lösung ist das Finden eines adäquaten mathematischen oder naturwissenschaftlichen Musters, das der Aufgabe am nächsten kommt.[33] Dazu braucht man die Fähigkeit
- des verstehenden Lesens, um den Inhalt zu erfassen
- des Analysierens, um die Komplexität der Aufgabenstellung zu bestimmen und einzelne Teilaufgaben abzuleiten,
- des Planens und Strukturierens, um Vorgehensweise und Abfolge festzulegen,
- des Bewertens, um die gefundene Lösung zu überprüfen, ob das gewonnene Ergebnis der Aufgabenstellung gerecht wird
In den USA wurden Studienergebnisse veröffentlicht, welche Probleme die Schüler im Physikunterricht haben.[34] Das Verstehen der Aufgabenstellung und des physikalischen Kontextes sind Voraussetzungen, um die Aufgaben erfolgreich zu bewältigen. Die Wissensanwendung baut auf das Vorhandensein effektiver Heuristiken zur Problemlösung. Die Leistungsfähigkeit des Arbeitsgedächtnisses und die Art und Weise, wie das Wissen (Informationen) im Langzeitgedächtnis des Schülers gespeichert ist, bestimmen, wie effektiv, die Aufgabe gelöst werden kann. Maßnahmen wie analoges Denken, Gruppenarbeit, stärkere Selbstreflexion, Durchdenken der Aufgabe mit externer Anleitung werden als probate Möglichkeit gesehen, den Schülern zum Lernerfolg zu verhelfen.
Das Trainieren der Mustererkennung und des Arbeitsgedächtnisses müssen der Schlüssel zu mehr Lernerfolg in der Schule sein. Hausaufgaben werden in der Schule erteilt, dass der Schüler sich mit dem im Unterricht vermittelten Wissen noch einmal beschäftigt, sich auseinandersetzt und verinnerlicht. Das Schreiben und das Durchführen von Experimenten unterstützen den Prozess der Wissensaneignung und Verinnerlichung des Wissens. Die Wissenschaft bestätigt die hier beschriebenen Erfahrungen:
Die meisten Forscher sind sich einig, dass die Mustererkennung auf der Grundlage von zuvor gespeichertem Wissen einer der Hauptgründe für die überlegene Leistung von Experten ist.[35]
Wie also können Kinder die Fähigkeit der Mustererkennung trainieren? Mit Schach werden spielend Fähigkeiten zur Filterung von Informationen und zur Mustererkennung trainiert. Das Schachspiel kann hervorragende Dienste als didaktisches Lerninstrument leisten.
2. Mustererkennung in Schulfächern wie Mathematik, Geometrie, Deutsch
„Der Mensch ist immer noch der beste Computer. (John F. Kennedy)“[36]
2.1. Mathematik in der Schule – Mustererkennung
Wie Wörter sich aus Buchstaben zusammensetzen, so setzen sich Zahlen aus Ziffern zusammen. Ausländer, die die deutsche Sprache erlernen, haben anfangs Mühe, wie der Deutsche Zahlen in Worten ausdrückt:
| Zahl | Deutsch | Englisch | Französisch |
| 21 | Einundzwanzig | twenty-one | vingt et un |
| 22 | zweiundzwanzig | twenty-two | vingt-deux |
| 233 | zweihundertzweiundzwanzig | two hundred and twenty-two | deux cent vingt-deux |
Der Deutsche nennt zuerst den Einer und dann den Zehner. Das führt zu Irritationen. Das kann bei Kindern mit Migrationshintergrund ein Problem darstellen, was durch Üben und aktives Sprechen ausgeräumt werden muss.
Jede Sprache hat ihre Besonderheiten. Die Zahlen 70, 80, 90 und 95 in der französischen Sprache gleichen einer Rechenaufgabe:
| 70 | soixante-dix | 60 + 10 |
| 80 | quatre-vingts | 4*20 |
| 90 | quatre-vingt-dix | 4*20 +10 |
| 95 | quatre-vingt-quinze | 4*20 + 15 |
Daraus kann nicht abgeleitet werden, dass die deutsche Sprache leichter oder schwerer als die französische Sprache ist oder dass die Kinder eines Landes leichter das Rechnen erlernen.
Beim Lösen von Mathematikaufgaben, gerade in den unteren Schulklassen, geht es, vereinfacht gesagt, um Mustererkennung. Es gibt viele Ratgeber und didaktische Hilfsmittel, die erklären, wie Kinder die Addition von Zahlen über den Zahlenraum größer 10 hinaus lernen. Dieser Aufgabe liegt letztlich die Mustererkennung zugrunde. Denn die Addition nach folgendem Muster:
10 + 1 =11
10 + 8 =18
20 + 7 = 27
60 + 9 =69
macht deutlich, dass man bei diesem Typus einfach die Einerstelle „0“ durch den einstelligen Summanden ersetzt, um die Lösung zu erhalten. D.h. man ersetzt das Bild „0“ durch das Bild des einstelligen Summanden. Dieses Muster kann dann auf kompliziertere Additionsaufgaben übertragen werden. Dabei kommen weitere Muster beim Kopfrechnen zum Einsatz.
Das Einmaleins muss verinnerlicht worden sein. Eine Grundschullehrerin alten Schlages erklärte es den Grundschülern einst so: „Wenn ich Dich nachts wecke und dir eine Aufgabe stelle, dann muss die Antwort sofort aus der Pistole geschossen kommen.“ Diese einfachen Grundaufgaben werden für die Lösung komplexerer Rechenoperationen herangezogen. Deshalb ist es wichtig, dass Kinder die gesamte Mathematikaufgabe ins Heft schreiben und dann erst die Lösung ergänzen. So prägen sie sich die Aufgabe als Musterbild ein.[37]
2.2. Wahrscheinlichkeitsrechnung – Musterkennung und geistige Vorwegnahme
Der Einstieg für die Wahrscheinlichkeitsrechnung erfolgt oft an Beispielen zu Münzwurf, dem Würfeln oder verschiedenfarbigen Kugeln in einer Kiste.
Im Praxistest erleben die Kinder: Je mehr Münzwürfe stattfinden, umso mehr nähert sich die Gensamtzahlen der Ereignisse „Zahl“ und „Wappen“ einander an – dem Verhältnis 50:50 bezüglich der Gesamtzahl der Würfe. Die Visualisierung kann durch Führen einer Strichliste für die jeweiligen Ereignisse „Zahl“ und „Wappen“ erfolgen.
Bei der Frage, wie hoch die Wahrscheinlichkeit ist, eine blaue Kugel zu ziehen, wenn sich in der Kiste 3 blaue Kugeln, 2 rote Kugeln und 5 grüne Kugeln befinden, muss zum Auffinden der richtigen Lösung planvoll vorgegangen werden. Die Erfahrung hilft begrenzt, denn man kann im Selbstversuch sofort mit dem ersten Griff eine blaue Kugel in der Hand halten als auch erst beim sechsten Griff in die Kiste. Nun kann man sich, ähnlich dem Münzwurf durch viele Versuche an das tatsächliche Ergebnis herantasten, was aber sehr zeitaufwendig ist. Vielmehr sollte ökonomisch gedacht werden, indem man nicht den Idealfall betrachtet, schon beim ersten Griff die blaue Kugel zu haben, was dann der Wahrscheinlichkeit Eins entspräche. Im Geiste spielt man die ungünstigen Szenarien durch. Dafür hilft es, sich die Kiste mit den farbigen Kugeln vorzustellen und zu visualisieren, welche Kugel in der Kiste verbleiben, wenn man eine Kugel herausnimmt. Man wird bemerken, dass zur Lösung der Aufgabe der ungünstigste Fall gefunden werden muss. Im vorliegenden Fall ist der ungünstigste Fall, dass zuerst alle roten und grünen Kugeln gezogen werden, ehe man mit Sicherheit eine blaue Kugel greift. Nun muss das gedankliche Ergebnis in der Sprache der Mathematik dargestellt werden.
Im Laufe der Mathematikausbildung in der Schule kommen neue Muster hinzu, die mit bisherigen kombiniert werden. Naturwissenschaftler greifen auf unterschiedliche „Rechentricks“ zurück, um Gleichungen und Brüche zu vereinfachen und zu lösen. Dabei geht es darum, komplizierte Terme auf einfachere Terme zurückzuführen, für die man Lösungsverfahren kennt. Typische Methoden sind Substitutionsverfahren, Verwendung der binomischen Formeln. Rechenvorteile zu erkennen und anzuwenden bedeutet: Selbstvertrauen in die eigenen Fähigkeiten zu besitzen sowie ein vorhandenes Spektrum an Lösungsmustern zu erweitern und zu optimieren.
2.3. Geometrie in der Schule – Musterkennung und Planung
Die Geometrie ist Mustererkennung pur. Anhand geometrischer Formen werden gern die Begriffe der Mengenlehre erklärt. Objekte mit gleichartigen Eigenschaften werden zu Mengen zusammengefasst.
| Gesamtmenge | Viereck | Trapez | Rechteck |
| Teilmengen | Parallelogramm | Parallelogramm | Quadrat |
| Rhombus | Rechteck | ||
| Rechteck | Quadrat | ||
| Quadrat | |||
| Trapez |
In der ebenen Geometrie ist ein Rechteck ein Viereck, dessen Innenwinkel alle rechte Winkel sind. Das bedeutet gleichzeitig, dass die gegenüberliegenden Seiten zueinander parallel verlaufen. Das Rechteck ist Spezialfall des Parallelogramms und damit auch des Trapezes. Beim Parallelogramm sind die gegenüberliegenden Seiten parallel. Die diagonal gegenüberliegenden Innenwinkel sind gleich groß. Beim Trapez sind 2 Seiten parallel zueinander. Ein Sonderfall des Rechtecks ist das Quadrat, bei dem zusätzlich alle Seiten gleich lang sind. Diese unterschiedlichen Bezeichnungen sind Teil der Fachsprache „Geometrie“, was nicht ausschließt, dass einige dieser Fachausdrücke in der Alltagssprache oft anzutreffen sind.
Beim Zeichnen maßstabsgerechter geometrischer Figuren muss die Vorgehensweise im Geiste geplant und die Abfolge der Schritte geprüft werden. Abhängig von den vorhandenen Angaben gibt es unterschiedliche Vorgehensweisen beim Zeichnen der geometrischen Formen.
Beispiel Dreieck
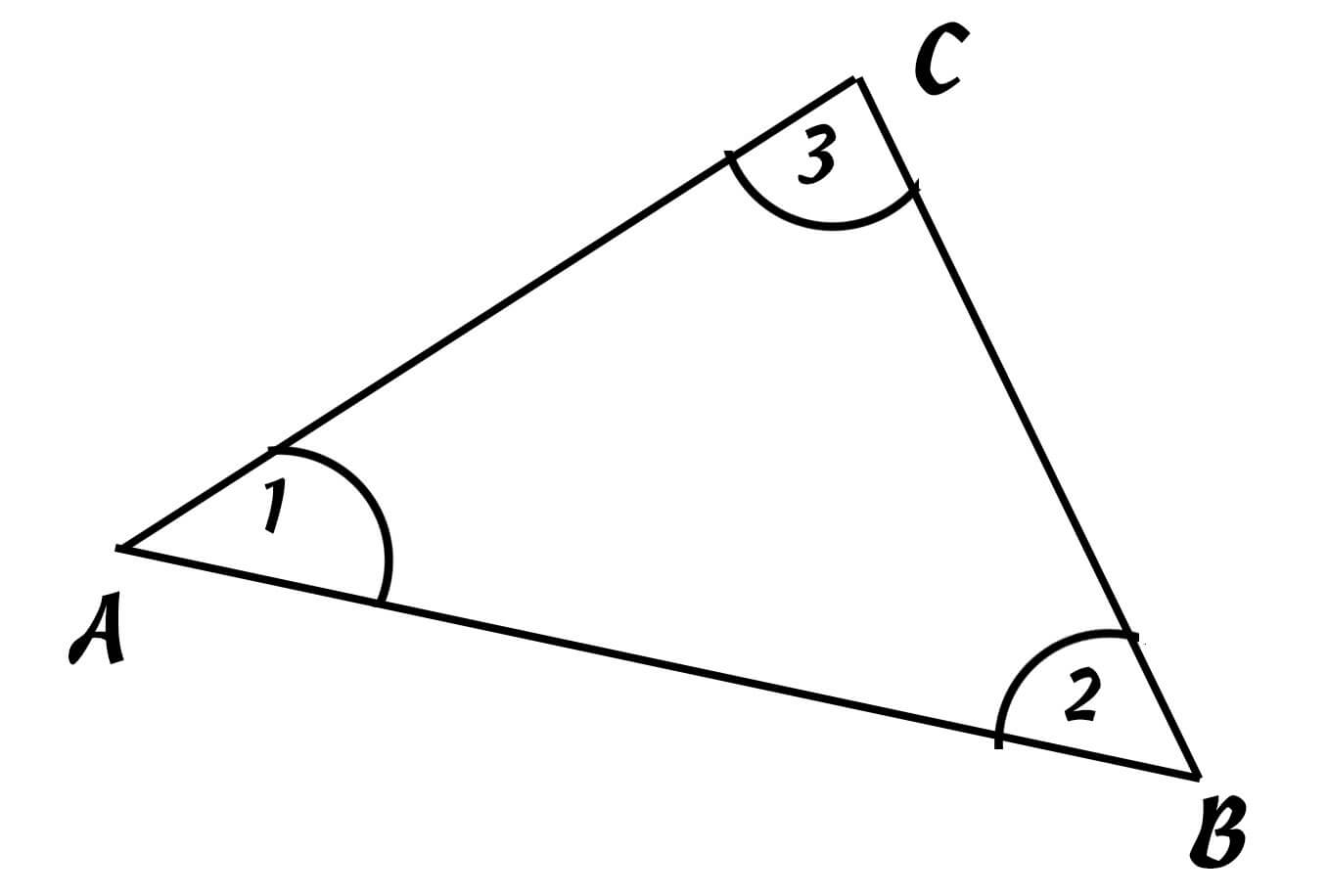
Wenn eine Seite (AB) und zwei Winkel (1,2) des Dreieckes ABC gegeben sind, dann wird nach folgendem Schema vorgegangen:
- Strecke AB (bekannte Seite) zeichnen
- eine Gerade durch den Schnittpunkt A mit dem Winkel 1 wird eingezeichnet
- eine Gerade durch den Schnittpunkt B mit dem Winkel 2 wird eingezeichnet
- Der Punkt C des Dreiecks ist der Schnittpunkt der Geraden aus 2. Und 3
Wenn alle Seiten des Dreiecks (AB, AC, BC) bekannt sind, aber nicht die Winkel:
- Strecke AB (bekannte Seite) zeichnen
- Mit dem Zirkel von Punkt A wird Kreisbogen mit Radius=AC gezeichnet
- Mit dem Zirkel von Punkt B wird Kreisbogen mit Radius=AB gezeichnet
- Der Schnittpunkt der beiden Kreisbogen aus 2. und 3. wird mit den Punkten A und B verbunden.
Die Mustererkennung erweist bei der Planung gute Dienste, indem man die bekannten Größen des Dreiecks visualisiert. Die Musterkennung, Visualisierung und geistige Planung der Verfahrensschritte führen auch in anderen Schulfächern zum Erfolg.
2.4. Sprache und Mustererkennung
Auch bei Sprache und Lesen geht es letztlich um Mustererkennung. Der einzelne Buchstabe hat gewöhnlich keine Bedeutung. Erst die Aneinanderreihung von mehreren Buchstaben ergibt ein Wort, was sowohl als visuelles Bild in Form des Wortes als Gesamtkombination aus einzelnen Buchstaben abgespeichert wird. Die Aneinanderreihung einzelner Laute, die Buchstaben oder Buchstabengruppen („sch“, „sp“ …) in der Bildsprache entsprechen, ergeben das ausgesprochene Wort. Die Aneinanderreihung ergibt ein Klangbild, was in Verbindung mit dem Objekt, dem Ereignis oder der Handlung abgespeichert ist. Das Klangbild der Wörter enthält zusätzliche Informationen im Vergleich zur schriftlichen Sprache und kann Gefühle auslösen. Aus dem Klangbild kann entnommen werden, ob es sich um eine Frage, Feststellung oder Aufforderung handelt, ob der Sprecher es eilig hat, ob es dem Sprecher langweilt oder interessiert, … Taube Menschen haben große Mühe, Wörter so auszusprechen, dass sie von ihren nichttauben Menschen mühelos verstanden werden. Den tauben Menschen fehlt die eigene Kontrollmöglichkeit, nämlich das Klangbild des Wortes zu vergleichen.
Im Gegensatz zur Mathematik kann man sich im Alltag ohne Kenntnis der Buchstaben und der Schreibweise verständigen, untereinander Informationen austauschen. Eine Fremdsprache kann ohne Kenntnis des Schriftbildes und der Buchstaben erlernt werden, wie man beispielsweise bei bilingual aufwachsenden Kindern beobachten kann. Da ist es unerheblich, ob es sich um eine Sprache handelt, die mit lateinischen Buchstaben oder kyrillischen Buchstaben visuell wiedergegeben wird. Für Hören und Sehen werden unterschiedliche Gehirnareale aktiviert.
Die Grammatik ist das Regelwerk der Sprache. Sie beschreibt u.a. wie die Zeitformen gebildet werden. Auch hier geht es um Musterkennung. In verschiedenen Sprachen wird zwischen regelmäßigen und unregelmäßigen Verben unterschieden. Die regelmäßigen Verben verfügen über feste Muster der Konjugation in den Zeitformen. Die Wortlehre liefert Muster und Methoden zur Wortbildung. So geben verschiedene typische Endungen Hinweise darauf, um welche Wortart es sich handelt ob es sich beispielsweise um ein Substantiv oder Adjektiv handelt:
| Typische Endungen für Adjektive | Typische Endungen für Substantive |
| -lich | -ung |
| -sam | -heit |
| -ig | -keit |
| -isch | -schaft |
| -bar | -tät |
| -haft | -tum |
| -arm | -nis |
3. Probleme bei der Messung des Lernerfolgs
Wie oben angedeutet wurde, ist der Wissenserwerb und die Steigerung der Schulleistungen ein sehr komplizierter Prozess mit vielen Einflussfaktoren. Trotz modernsten wissenschaftlicher Methoden und Techniken wird es keine hundertprozentige Sicherheit in allen Details geben.
Das Hauptproblem der Studien im Bildungsbereich ist generell, dass die Studienteilnehmer nicht einfach mal für eine gewisse Zeit isoliert werden können. Vielmehr befinden sie sich im permanenten Austausch mit ihrer Umgebung, unterliegen Launen und Stimmungsschwankungen, haben täglich wechselndes Wohlbefinden und wechselnde energetische Zustände.
Nicht alle Lehrende verstehen es gleich gut, die Schüler für das Unterrichtsfach oder das Schachspiel zu begeistern und mitzureißen. Es gibt Schüler, die eine Abneigung gegenüber dem Lehrenden haben und in der Folge wenig Motivation zum Lernen zeigen und sich in geringerem Maße um gute Resultate im Unterrichtsfach bemühen. Die Kinder befinden sich noch in der Wachstumsphase, d.h., mit zunehmenden Alter treten Veränderungen in Wahrnehmung, Sicht- und Verhaltensweisen ein. Jeder Mensch bringt von Natur aus unterschiedliche Voraussetzungen in Form seiner Gene mit. Die Forscher stehen bei der Entwicklung geeigneter Versuchsdesigns zur Überprüfung der Wirksamkeit von Maßnahmen zur Steigerung des Lernerfolgs vor immensen Herausforderungen.
Die Anforderungen in den Ausbildungsberufen und Studienrichtungen unterliegen Veränderungen. Die Wissensvermittlung muss sich den ändernden Bedingungen anpassen. Wissensvermittlung ist seit jeher eine Herausforderung. Allerorten werden Fachkräfte gesucht, die auch noch verschiedene Persönlichkeitsmerkmale mitbringen sollen. Gerade in der Bildung zeigt sich, dass viel Geld nicht automatisch viel hilft.
Entscheidungsträger in Politik, Wirtschaft und Verwaltung mögen konkrete Zahlen und Ergebnisse, die belegen, dass sich die gewünschten Ergebnisse auch einstellen werden. Wenn die Idee „Schach in der Schule“ zur Verbesserung schulischer Leistungen dargelegt wird, folgt sehr oft die Nachfrage nach Beweisen zur Wirksamkeit von Schach für mehr Lernerfolg. Es gibt hunderte Studien, die den Lernerfolg von Schach belegen und jede Studie hat hinsichtlich des Versuchsdesigns Stärken und Schwächen.
Wie sieht es bei aktuellen Themen in der Schule aus? Welche gesicherten wissenschaftlichen Erkenntnisse gibt es zur Wirksamkeit verschiedener Unterrichtsmaßnahmen, zum Beispiel dem fächerübergreifenden Unterricht? Welche Erkenntnisse gibt es für die Wirksamkeit der Verlängerung der Unterrichtsstunde von 45 Minuten auf 60 oder 90 Minuten hinsichtlich der wünschenswerten Ziele von mehr Wissenszuwachs und mehr Lernerfolg, vor allem vor dem Hintergrund, dass die Pädagogen immer wieder die mangelnde Konzentrationsfähigkeit und fehlende Aufmerksamkeit bei den Schülern beklagen? In einer in 2021 veröffentlichten Studie heißt es: „Empirische Erkenntnisse darüber, ob sich die mit dem veränderten Stundentakt verbundenen Erwartungen bestätigen, liegen für das deutsche Schulsystem bisher kaum vor.“[38] Anschließend wurden die Ergebnisse von drei untersuchten Gymnasien (125 Lehrkräfte und 803 Schüler) vorgestellt. In der genannten Studie wurde nicht dargelegt, ob die Verlängerung der Unterrichtsstunden zu besseren Wissensständen und besseren Noten bei den Schülern führte, wie sich die verlängerte Unterrichtsstunde auf die Konzentration und Aufmerksamkeit der Schüler auswirkt. Wie wirkt sich die längere Unterrichtstunde an den Grundschulen, Mittel-, Real- und Oberschulen aus, wo mehr leistungsschwache Schüler lernen als an Gymnasien?
Der fächerübergreifende Unterricht wird seit sehr vielen Jahren propagiert und in den Schulen umgesetzt. Ziel des fächerübergreifenden Unterrichts ist der Wissenstransfer und die Verknüpfung von vorhandenen Wissen. Jetzt, in 2022, resümieren Haunhorst et al: „Die Lehramtsstudierenden erlangen vielfältige Kompetenzen im Unterrichten der eigenen Fächer, jedoch wenige Kompetenzen im fächerübergreifenden Unterricht.“[39] Weiter wird festgestellt, dass die Datenlage unzureichend ist und dass es große Probleme bei der Konzipierung eines Forschungsdesigns zur Evaluation des fächerübergreifenden Unterrichts gibt. Als Bedingung für den Erfolg wird die Notwendigkeit angesehen, den Lerngegenstand aus unterschiedlichen Perspektiven und Herangehensweisen zu betrachten. Weitere notwendige Bedingungen sind die fachliche Kompetenz der Lehrenden und die Fähigkeit der Lehrenden untereinander im Sinne des fächerübergreifenden Unterrichts zu kooperieren. Für den fächerübergreifenden Unterricht mit der Kombination „Sport und naturwissenschaftliches Unterrichtsfach“ wurden für die Jahre von 2000 bis 2019 im Fachportal Pädagogik insgesamt 14 Studien erfasst.[40]
Anders im Schach. Es gibt hunderte Studien, die den Einfluss von Schachunterricht auf den Lernerfolg in der Schule untersuchten. Trotz des Wissens um die Problematik der Durchführung wissenschaftlicher Studien über Einflüsse auf den Lernerfolg, herrscht weitgehender Konsens darüber, dass sich Schachunterricht positiv auf kognitive Fähigkeiten und die Leistungen in den Schulfächern auswirkt.[41]
Für die in 2022 veröffentlichte Studie über die „Verbesserung der kognitiven Fähigkeiten und schulischen Leistungen infolge des Schachunterrichts“[42] wurden hohe Anforderungen an die zu untersuchenden Studien gestellt. Drei Hauptkriterien wurden für das Untersuchungsdesign formuliert. 230 relevante wissenschaftliche Studien wurden in den Datenbanken identifiziert, wovon 45 Studien den drei Hauptkriterien genügten.
Es wird nicht bezweifelt, dass Schach positive Auswirkungen auf die Schulleistungen hat. Die Kritik an den untersuchten Schachstudien richtet sich darauf, dass diese sich zu sehr auf die Erfolgsmessung von weitem Transfer (far transfer) konzentrierten, die Stichprobenumfänge eher niedrig waren und eher kurzfristige als langfristige Auswirkungen untersucht wurden.[43] Auch die Untersuchungen im Bildungs- und Schulbereich, die keinen Bezug zu Schach aufweisen, stehen in der Kritik, weil sie eher die kurzfristigen Auswirkungen untersuchen. Watts et al.[44] sind der Meinung, dass fehlende Studien mit langfristigen Nachverfolgungen Schwierigkeiten für das Entwickeln gut wirkender Bildungsprogramme darstellen. Die Forscher bemängeln, dass derzeit Zusammenhänge zwischen kurzfristigen Ergebnissen und langfristigen Auswirkungen oft angenommen, aber selten mit experimentellen Methoden überprüft werden.
Blanch untersuchte die Ergebnisse von 45 ausgewählten Studien aus 19 Ländern (Argentinien, Australien, Bangladesch, Belgien, Kanada, Dänemark, Deutschland, Indien, Iran, Italien, Malaysia, Rumänien, Südafrika, Südkorea, Spanien, Türkei, Großbritannien, Uruguay und USA)[45]. Die beiden Länder Russland und Brasilien, die zu den aktivsten Ländern im Schulschach weltweit zählen, fanden keine Berücksichtigung. Auf dem in 2018 stattgefundenen internationalen Kongress zur psychischen Gesundheit des Menschen im 21. Jahrhundert, an dem Wissenschaftler u.a. aus Deutschland, USA, Großbritannien, Chile, Portugal, Malaysia, Indien teilnahmen, wurden die Ergebnisse einer Langzeitstudie zur Wirkung des Schachunterrichts auf die intellektuelle Entwicklung der Kinder über die Schullaufbahn hinweg veröffentlicht.[46] Die Studie untersuchte die Nahtransfereffekte. De Ergebnisse sind beeindruckend und werden im nächsten Abschnitt dargelegt.
4. Langanhaltende Leistungserfolge beim Lernen durch Schachspielen
„Ein Lernschritt kann hundert Entwicklungsschritte bedeuten.“ (Lev Vygotsky)[47]
In Russland wird das Unterrichtsfach „Schach“ als Chance gesehen, den Schülern optimale Möglichkeiten für ihre Entwicklung und schulischen Lernerfolg zu schaffen. Seit 2004 läuft eine Langzeitstudie über die Auswirkungen des Schachunterrichts auf die persönliche und schulische Entwicklung mit verschiedenen Schulen in der Stadt Satka (Oblast Tscheljabinsk). In 18 Jahren wurden 1571 Schüler in der Studie untersucht, wobei 723 Schüler nach dem Lehrprogramm „chess project“ unterrichtet wurden, welches auf Basis der Ideen des Psychologen Lev Vygotsky (Lew Wygotski), der Prinzipien des reflexiven Aktivitätsansatzes[48] und des russischen Bildungsziels „im Geiste zu handeln“[49] entwickelt wurde. „Im Geiste handeln“ bedeutet, in Gedanken verschiedene Möglichkeiten und Prozesse durchspielen und dabei prüfen was geschieht, wenn ein Schritt gemacht wird, welcher weiterer Schritt als Konsequenz folgen könnte und wie er sich auswirkt. Die Gestaltung des Schachunterrichts auf Basis der Prinzipien des reflexiven Aktivitätsansatzes soll die Schüler befähigen, die im Schachunterricht entwickelten Fähigkeiten bewusst auf andere Schulfächer und Aktivitäten zu übertragen. Dieser Transfer wirkt sich auf die allgemeine Entwicklung des Schülers aus, wirkt präventiv gegen Schulversagen und spiegelt sich in besseren schulischen Leistungen wieder.
Mit wissenschaftlicher Begleitung wurden Schachlehrbücher, Arbeitsbücher und ein Schachprogramm für das Schulprojekt. Die englische Version der Lehrmaterialien und erste Ergebnisse der Studie wurden 2017 in Quebec (Kanada) auf dem internationalen Kongress „Contemporary Russian Contributions to Vygotsky’s Heritage“, der von International Society for Cultural-Historical Activity Research (ISCAR) ausgerichtet wurde, einer breiten Öffentlichkeit vorgestellt.[50] In den Folgejahren wurden weitere Ergebnisse der Schachstudie der Öffentlichkeit zugänglich gemacht.
Umfangreiche Informationen zu den ersten Phasen der aufwendigen Schulschach-Studie mit vielen zusätzlichen theoretischen Erläuterungen wurden 2022 publiziert.[51] In den ersten beiden Phasen wurden 637 Schüler untersucht, von denen 331 an dem genannten Schachprogramm teilnahmen.
Ergebnisse der ersten Phase 2004 – 2008 (Grundschulzeit)
Die Schüler mit Schachunterricht gemäß dem Lehrprogramm „Schach für die allgemeine Entwicklung“ (chess-project) machten größere Fortschritte als die Kinder aus den Kontrollgruppen. Sie zeigten ausgeprägtere Fähigkeiten für das Lernen nach Gehör, verbesserten ihr visuelles Gedächtnis, kamen besser mit Aufgaben des nonverbalen Denkens zurecht, wurden aufmerksamer, effizienter und konnten ihre Handlungen besser gedanklich planen, wie die verwendeten Tests zur Aufdeckung des inneren Handlungsplans zeigten. Die Ergebnisse für drei dieser Indikatoren stiegen im Laufe des Jahres stetig an, was sich in jeder Untersuchung zeigte: das akustische Gedächtnis, die verbale Intelligenz und der interne Handlungsplan. Für keinen der Indikatoren wurde eine negative Dynamik festgestellt. Keine der Vergleichsgruppen wies bei einem der Indikatoren einen derart auffälligen Trend auf.
Ergebnisse der zweiten Phase 2010 – 2013
Hier wurden zwei Aufgabenstellungen verfolgt:
-
-
- Beobachtung der Entwicklungsdynamik von Kindern in einer gemischten Klasse, in der vier Kinder mit Entwicklungsstörungen waren. Alle werden gemeinsam nach dem Lehrprogramm „Schach für die allgemeine Entwicklung“ (chess-project) unterrichtet.
- Prüfung, ob das hohe Entwicklungsniveau der kognitiven Funktionen bei Kindern erhalten bleibt, die in der Grundschule am Schachunterricht mit dem Programm „chess project“ teilnahmen, im Vergleich zu den Gruppen die am Programm „chess universal“[52] teilnahmen und die gar keinen Schachunterricht bekamen. Die untersuchten Neuntklässler haben seit 2004 am Schachprojekt und an psychologischen Untersuchungen teilgenommen.
-
Ergebnisse zu den beiden Aufgabenstellungen
-
-
- Aus den Ergebnissen der Erhebung lässt sich schließen, dass die Zweitklässler in der Hauptgruppe eine positive Entwicklungsdynamik bei 5 Indikatoren aufweisen: Gedächtnis (auditiv und visuell), nonverbale Intelligenz, Arbeitsfähigkeit und die Fähigkeit, Handlungen im Kopf zu planen. In Bezug auf diese Indikatoren besteht ein statistisch signifikanter Unterschied zwischen der Erhebung vom Mai 2011 und der Erhebung von 2012.
-
Die Ergebnisse bei den Kindern mit Entwicklungsstörungen fielen unterschiedlich aus, wobei einige Indikatoren höhere Werte zeigten,
-
-
- Der Vergleich der Ergebnisse der Hauptgruppe „chess project“ und der Gruppe „chess universal“ zeigte, dass die Hauptgruppe einen höheren Entwicklungsstand der nonverbalen Intelligenz und höhere Aufmerksamkeitswerte aufwies.
-
Über den angegebenen Zeitraum hat eine große Anzahl von Schülern, sowohl Schachschüler als auch Nicht-Schachschüler, ihr kognitives Entwicklungsniveau generell verbessert. Allerdings haben die Schüler der Hauptgruppe im Vergleich zu den Kontrollgruppen, in denen Schach mit anderen Methoden oder gar nicht unterrichtet wurde, ihre Ergebnisse bei einer Vielzahl von intellektuellen Indikatoren im Laufe der Jahre stetig verbessert.
Den Daten zufolge zeigen schachspielende Schüler mit unterschiedlichem intellektuellem Entwicklungsstand eine positive Dynamik in der Entwicklung der intellektuellen Fähigkeiten. Eine vergleichende Analyse der Indikatoren ergab ein hohes Maß an Effektivität des Schachunterrichts auf der Grundlage des reflexiv-aktivierenden Ansatzes verwendet.
Wie die Ergebnisse der dritten Phase (siehe unten) gezeigt haben, wirkte sich die positive Entwicklung der geistigen Fähigkeiten in der Primar- und Sekundarstufe positiv auf die Lernleistungen in verschiedenen Fächern aus.
Ergebnisse der dritten Phase 2014 – 2021
Die positive Wirkung des Schachunterrichts war noch größer als gedacht. Die Schüler wurden selbstbewusster, lernten, ihre Aufgaben selbstständig zu planen, konnten ihre Erfolge und Misserfolge reflektieren, ihre Einstellung zu Fehlern änderte sich und ihr persönliches Potenzial im Hinblick auf die Selbstwirksamkeit wurde gesteigert. In der Folge erreichten die Schüler gute schulische Ergebnisse. Die Zahl der Schulabsolventen, die Medaillen für besondere Lernleistungen erhielten, stieg.
Angesichts der positiven Ergebnisse in der dritten Phase wurden weitere Faktoren in die Untersuchung einbezogen, um mehr zu erfahren über Lernmotivationen, über das selbständige Bewältigen schwieriger Situationen, Schulangst u.a. Seit 2017 wird auch in dieser Richtung geforscht. Die Arbeit an der Analyse aller diagnostischen Ergebnisse geht weiter und wird in weiteren Publikationen vorgestellt werden.
5. Schach fördert Inklusion nachhaltig
Die besonderen Eigenschaften des Schachspiels machen das Spiel auch zum Zwecke der Therapie interessant. Seit einigen Jahren ist weltweit ein Trend zu beobachten, das Schachspiel in der Therapie einzusetzen, neue Therapieformen zu entwickeln und Heilungserfolge zu erzielen. Im Fokus bei der Behandlung mittels dem Schachspiel stehen Kinder, die unter bipolaren Störungen, Depressionen, ADHS und Verhaltensstörungen leiden.[53]
Die Zahl der Kinder, bei denen ADHS diagnostiziert wird, nimmt von Jahr zu Jahr zu. Wissenschaftliche Studien sehen einen Zusammenhang zwischen extensiver Benutzung des Smartphones/ des Internets und der Diagnose ADHS.[54] Aufmerksamkeitsstörungen wie ADHS wirken sich negativ auf die schulischen Leistungen aus. Die bei ADHS verordneten Medikamente belasten die Sozialsysteme finanziell und weisen unliebsame Nebenwirkungen auf. Wenn extensive Smartphone-Nutzung der Grund für ADHS ist, dann sollte Aussicht bestehen, die ADHS-Einschränkungen wenigstens deutlich zu lindern, weil Aufmerksamkeit trainiert werden kann. Regelmäßiges Schachtraining zur Verbesserung der Aufmerksamkeit reduziert die Probleme von ADHS, wie ein großer Studienvergleich ergab.[55] 2021 wurde die erste klinische Studie veröffentlicht, in der nachgewiesen wird, dass regelmäßiges Schachtraining als Therapie die kognitiven Leistungen von ADHS-Patienten deutlich verbesserte. Die Patienten berichten, dass ihre allgemeine Stimmung und die zwischenmenschlichen Beziehungen sich verbesserten.[56]
Deutsche Wissenschaftler waren eine der ersten weltweit, die 2008 eine Studie[57] vorstellten, die die Auswirkungen des Schachunterrichts in Klassen von Kindern mit Lernschwierigkeiten untersuchte. Ziel dieses vergleichenden Ansatzes war es, ob die besondere Lehrmethode des Schachspiels im Mathematikunterricht für Kinder mit Lernschwierigkeiten zu besseren Lernerfolgen führt. Das Schachspielen soll die Schüler zu einer verbesserten Aufmerksamkeit verhelfen und in der Folge zu höheren mathematischen Grundfertigkeiten bei den Kindern mit Lernbehinderungen führen. Die Versuchsgruppe tauschte eine Mathematikstunde gegen eine Schachstunde ein. Am Ende des Schuljahres wurden die Verbesserungen der Rechen- und Konzentrationsfähigkeiten der Kinder zwischen der Versuchsgruppe, die Schachunterricht anstelle einer Stunde regulären Mathematikunterrichts pro Woche erhielt, und einer Kontrollgruppe, die nur regulären Mathematikunterricht erhielt verglichen. Die Versuchsgruppe war bei der Verbesserung der mathematischen Grundfertigkeiten wie Zählen und Addieren eindeutig im Vorteil. Schach als Element des Mathematikunterrichts in Schulen für Kinder mit Lernschwierigkeiten kann eine wertvolle Lernhilfe sein.
Das Thema Inklusion ist auch in Deutschland angekommen. Ziel ist es, Menschen mit Behinderung eine gleichberechtigte Teilhabe an der Gesellschaft zu ermöglichen. Kinder mit geistiger Behinderung auf ein selbstbestimmtes Leben vorzubereiten ist eine äußerst schwierige Aufgabe. Wie kann man ihnen den Weg zu einem Beruf ebnen, mit dem sie ihren eigenen Lebensunterhalt verdienen können? Auch hier gibt es beeindruckende Ergebnisse, wie Schach scheinbar fest vorgezeichnete Lebenswege komplett verändert und Träume wahr werden lässt:
2022 sorgte ein deutscher Behinderter für fantastische Schlagzeilen:
„Und dann wird Jarno Scheffner Weltmeister
Er gilt als „geistig behindert“. Aber als er mit elf Jahren anfängt, Schach zu spielen, verändert das sein ganzes Leben.“
(11.08.2022, Zeit online)[58]
Zur Person Jarno Scheffner: Er hat einen IQ von 59 und geht auf eine Förderschule für geistig Behinderte. Ein Lehrer bringt ihm das Schachspiel bei und er liebt dieses Spiel. Heute arbeitet er als Gärtner.
Und die andere gute Nachricht ist, dass offenbar mit systematischen Schachtraining Kindern mit Entwicklungsstörungen geholfen werden kann. Das Schachprojekt in der russischen Stadt Satka (Oblast Tscheljabinsk) macht Hoffnung (siehe vorhergehenden Abschnitt).
Die ebenfalls in 2022 publizierte Schachstudie von Sidorenko[59] ist ein weiteres Beispiel für die Mächtigkeit des Lerninstruments Schach in Verbindung mit dem reflexiven Aktivitätsansatz. In 10 Monaten Schachunterricht und mit anderen Rehabilitationsmaßnahmen hat ein 30-jähriger Mann einen erstaunlichen Weg zurückgelegt. Zu Beginn führte der Mann das Leben eines gewöhnlichen Bewohners eines psychoneurologischen Internats und war als rechtlich geschäftsunfähig eingestuft Er nahm Medikamente, ohne Aussicht auf Verbesserung seines Zustandes, war ohne Zukunftsperspektive. Nach 10 Monaten Schachtraining ist er bereits ein anderer Mensch: Er lebt mit seiner Familie statt im Internat, kommt ohne Medikamente aus, arbeitet, schmiedet berufliche Pläne und will heiraten. Das Hauptziel – die Wiederherstellung der Geschäftsfähigkeit – wurde erreicht. Dieser Einzelfall zeigt, dass das in Satka entwickelte Schachlehrprogramm mit Unterstützung von Psychologen auch behinderten Menschen den Weg in ein selbstbestimmtes Leben ermöglichen kann.
6. Warum Schach sich positiv auf Mathematik und die MINT-Fächer auswirkt
Die immer schlechter werdenden Lernergebnisse deutscher Schüler verlangen ein Gegensteuern. Es stellt sich die Frage, ob man neuartige Konzepte erfinden muss oder ab man auf schon vorhandene Konzepte, die wissenschaftlich gestützt werden, zurückgreift.
Aus philosophischer Perspektive kann Schach als Mathematik betrachtet werden: „Schach ist Mathematik, weil es rein relational ist: Schachfiguren haben keine anderen Funktionen als die, die sie im Spiel erfüllen (ihre Form erinnert lediglich daran, um welche Figur es sich handelt). Schach wird normalerweise nicht als ernsthafte Mathematik angesehen, weil die Regeln willkürlich gewählt werden (und weil die Frage, was eine gute Strategie im menschlichen Schach ausmacht, von einer äußeren, kontingenten Tatsache abhängt, nämlich der Intelligenz der Spieler). Aber die Existenz einer Springertour über das gesamte Schachbrett, die Lösbarkeit von in Zeitungen veröffentlichten Schachaufgaben mit einer bestimmten Konfiguration und der Anweisung „Schwarz setzt in zwei Zügen matt“ und die Fähigkeiten von AlphaZero[60], Schach auf übermenschlichem Niveau zu spielen, sind allesamt reine Mathematik.“[61]
Soweit die Theorie. Doch was passiert während einer Schachpartie im Gehirn des Menschen? Je mehr man sich mit den Prozessen, die während der Schachpartie ablaufen, beschäftigt, umso mehr Faktoren erkennt man, die auch für den Lernerfolg in der Schule vorteilhaft sind. Das Trainieren der Mustererkennung und der Einfluss regelmäßigen Schachtrainings auf die Persönlichkeitsentwicklung scheinen die stärksten Faktoren zu sein. Sie sind auch die Faktoren, die am schwierigsten zu messen sind. Es werden einige Prozesse, die während einer Schachpartie stattfinden, genauer betrachtet.
Die Hirnforschung fand heraus, dass das menschliche Gehirn Bilder 60.000-mal schneller als Text verarbeitet. 90 Prozent aller Informationen, die an unser Gehirn übermittelt werden, sind visuell. Wie oben dargelegt wurde, kann Mathematik als die Wissenschaft von Mustern aufgefasst werden. Um erfolgreich in Mustererkennung zu sein, braucht das Gehirn eine riesige Bibliothek an Bildern und Mustern, die mit zusätzlichen Informationen wie Erfahrung, Nützlichkeit und Verknüpfungen zu anderen Bibliotheksinhalten versehen sind.
Schach bietet gute Voraussetzungen, um das Gehirn spielerisch in Mustererkennung zu trainieren. Das Schachspiel ist sehr komplex. Bei jedem Zug muss eine enorme Menge an Informationen verarbeitet werden. Bei der Vorausberechnung von mehreren Zügen müssen unterschiedliche Bewegungsmuster der Schachfiguren verarbeitet werden. Schachspieler entwickeln Fähigkeiten, um mit der Informationsflut zurechtzukommen, mit den Ressourcen des Gehirns ökonomisch umzugehen. Im Mittelpunkt steht die effiziente Auswahl an Schachzügen, die es wert sind, genauer analysiert zu werden. Der Schachspieler muss unablässig Informationen aufnehmen, filtern, sortieren, verarbeiten, bewerten und entscheiden. Bei Schachpartien von Mensch zu Mensch können zusätzliche Informationen zur Bewertung des Schachzuges aus dem Verhalten des Gegners gewonnen werden: Schwitzen, Gesten, Nervosität, Körperhaltung.
Nach dem Schachspiel folgt die gemeinsame Analyse, in der letztlich die zuvor getroffenen Entscheidungen in der Partie überprüft und bewertet werden. Bei der Analyse legen die beteiligten Personen ihre Gedankengänge, ihre Vorgehensweise zur Zugauswahl und Zugbewertung offen. Es werden zusätzlich die Sprachkompetenzen trainiert, sich treffsicher und verständlich auszudrücken, vorgebrachte Argumente zu verstehen, zu bewerten und zu übernehmen. Aus groben Fehlern wird schneller gelernt, weil typische Muster schneller wiedererkannt und demzufolge leichter vermieden werden können. Im gemeinsamen Spiel und der gemeinsamen Analyse erwerben die Kinder Kompetenzen in Teamfähigkeit, also anderen aufmerksam zuhören, das Gesagte reflektieren, sich aktiv in den Meinungsbildungsprozess einbringen, respektvoll miteinander umgehen. Bei der gemeinsamen Analyse kommt es immer wieder vor, dass Züge zum Partiegewinn vorgeschlagen werden, die sich offensichtlich als Fehler entpuppen, weil übersehen wurde, dass der Gegner einfach Schachfiguren gewinnt und später die Partie, die Drohung nicht fürchten muss, die vorgeschlagene Kombination fehlerhaft ist. Das passiert auch erfahrenen Schachspielern. Weil diese Fehler jedem irgendwann einmal unterlaufen kann, möchte keiner, dass er deshalb schlecht behandelt wird. So lernt man in der Gruppe, respektvoll miteinander umzugehen.
Dass Schachspieler Strategien zur effizienten Informationsverarbeitung und Mustererkennung entwickeln müssen, machen folgende Zahlen deutlich: In der Grundstellung muss sich Weiß zwischen 20 möglichen Zügen (16 Bauernzüge und 4 Springerzüge) entscheiden. Nach dem ersten Zug von Weiß stehen Schwarz ebenfalls 20 mögliche Züge (16 Bauernzüge und 4 Springerzüge) zur Verfügung, denn seine Figuren befinden sich noch in der Grundstellung. Es gibt 20 x 20 = 400 verschiedene Schachstellungen nach zwei Zügen (erster Zug für Weiß, gefolgt vom ersten Zug für Schwarz). Es gibt 5.362 verschiedene Schachstellungen nach drei Zügen (zweiter Zug von Weiß). Es gibt 71.852 verschiedene Schachstellungen nach vier Zügen (zwei Züge für Weiß und zwei Züge für Schwarz). Nach 5 Zügen sind es schon 809.896 verschiedene Stellungen und nach 6 Zügen (drei Züge für Weiß und drei Züge für Schwarz) sind es schon 9.132.484 verschiedene Stellungen.
Die Aufmerksamkeitsspanne bei Kindern sank in den letzten Jahren als Folge intensiver Smartphone- und Internetnutzung rapide. „Allein die räumliche Anwesenheit unseres eigenen Smartphone – mit allen seinen fantastischen Optionen der Ablenkung – führt zu einer Schwächung unserer kognitiven Leistungsfähigkeit.“[62] Die Kinder lernen beim Schachspiel sich auf die Ereignisse auf dem Schachbrett zu konzentrieren. Als ein Grund kann der kompetitive Charakter des Schachspiels gesehen werden, weil die Kinder besser werden wollen. Ein anderer Grund ist das Erleben von Erfolg, d.h., ich passe im Schachunterricht auf, dann mache ich weniger Fehler im eigenen Spiel und gewinne mehr Partien. „Aufmerksamkeit stellt in der heutigen Informationsgesellschaft eine wichtige persönliche Ressource dar und ist entscheidend für persönliche Leistungsfähigkeit, Motivation und Problemlösungsfähigkeit und zwar in allen Altersstufen.“[63] Der kompetitive Charakter des Schachspiels weckt in den Kindern den Ehrgeiz, besser zu werden, als die anderen, d.h., sie sind motiviert zu lernen.
Studien zum Einfluss des Schachunterrichts auf die Mathematik stellen einen positiven Zusammenhang zur Arithmetik fest. Die schachspielenden Kinder lernen, dass die Figuren unterschiedliche Wertigkeiten haben und dass eine Leichtfigur (Springer oder Läufer) dem Wert von drei Bauern entspricht. Die Kinder lernen in der figürlichen Schachumgebung Grundrechenaufgaben und typische mathematische Sachverhalte wie Substitution, Verhältnis und Äquivalent. Die Kinder begreifen schnell, dass ein Turm im Wert zwei Leichtfiguren entspricht, dass dann eine Leichtfigur mit drei Bauern dem Turm gleichwertig sind, zumindest mathematisch gesehen.
Rechenbeispiele mit Schachfiguren:
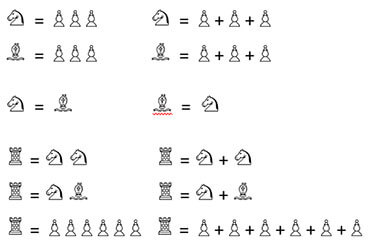
Der Gedankenprozess für die quantitative Bewertung der auf dem Schachbrett befindlichen Figuren bereitet die Kinder auf das Rechnen mit Variablen und das Lösen von Aufgaben mit mehreren Unbekannten vor, weil die Kinder mittels dem Schachspiel schon erste Erfahrungen mit diesen Mustern und Denkweisen sammelten.
Wenn die Kinder anfangen Schach zu lernen. wird zuerst das Schachbrett und die Orientierung darauf ausführlich erklärt. Sie erfahren, dass jedes Feld einen Namen hat, der sich aus einem Buchstaben von A bis H und einer Zahl von 1 bis 8 zusammensetzt, was die Koordinaten des Schachfeldes sind. Und diese Form der Identifizierung von Feldern und der Orientierung auf dem Schachbrett erleichtern das Lesen von Landkarten, Diagrammen und Kurvenverläufen. Es dürfte immer weniger Kinder geben, die schon einen Stadtplan oder eine Landkarte in der Hand hielten. Das bequeme Navigationsgerät im Auto oder im Handy verdrängte die Landkarte. Im Navigationsgerät gibt man den gesuchten Ort ein und schon blinkt an einer Stelle auf dem Bildschirm ein Kreis.
6.1. Schachspieler denken in Bildern
Der Schachspieler muss eine Unmenge an visuellen Informationen auf dem Schachbrett verarbeiten und daraus sein konkretes Handeln, den nächsten Schachzug auszuführen, ableiten. Es gilt zu erkennen, ob eine Figur geschlagen werden kann und ob man dafür einen Gegenwert erhält, welche konkreten Drohungen vorhanden sind oder der Gegner plant und inwieweit diese mit den eigenen Plänen kollidieren. Und schließlich muss er in der erfassten Situation den besten Zug auswählen, sich entscheiden, den einen Zug auszuführen. Dazu muss er vor dem geistigen Auge mögliche Zugfolgen ablaufen lassen und die dann jeweils entstehenden Partiestellungen bewerten. Bei den Zugabläufen müssen unterschiedliche Bewegungsmuster der eigenen und der gegnerischen Figuren berücksichtigt und zusammengefügt werden. Zur Bewertung greifen erfahrene Schachspieler auf Erfahrungen und bekannte Stellungsmuster zurück, die im Gehirn abgespeichert sind.

Schachfiguren „Flamenco“, gefertigt aus Hufnägeln, Schraubenteilen und Gabeln
Das Taktiktraining, also das Lösungen von Schachaufgaben wie „Matt in einem Zug“ oder „Matt in zwei Zügen“ oder „Weiß am Zug gewinnt“ trainiert das Sehen. Das Gehirn prägt sich Stellungsmuster und dazugehörige Gewinnverfahren ein. Je mehr Taktikaufgaben gelöst werden, umso eher ist der Spieler in der Lage, zugrundeliegende Muster (Gabel, Doppelangriff, schwache Grundreihe, …) zu erkennen, zu abstrahieren und in eigenen Partien anzuwenden. Die auf dem Schachbrett entstandene Stellung wird mit den im Gehirn abgespeicherten Gewinnstellungen und Gewinnmusterverfahren verglichen, um zu bewerten, ob beispielsweise die Voraussetzungen für einen erfolgreichen Mattangriff vorhanden sind und ob das bekannte Gewinnverfahren direkt oder in abgewandelter Form angerwendet werden kann. Die Stellungstransformation wie den Übergang vom Mittelspiel in ein leicht zu gewinnendes Endspiel baut auf ein tiefer gehendes Verständnis der Schachstellung. Es geht im Schach letztlich immer wieder um Mustererkennung. Die Erfahrung zeigt, dass beispielsweise freie Linien, Freibauern, gedeckter Freibauer, Raumvorteil gute Voraussetzungen für die siegreiche Gestaltung der Schachpartie sind. Bei der Entscheidung über den nächsten Zug, muss der Spieler vor seinem geistigen Auge Pläne, also gewünschte Schachstellungen, entwickeln, die er erreichen will. Dazu muss er verschiedene Zugabläufe prüfen, also unterschiedliche Bewegungsmuster der Figuren, sowohl der eigenen als auch der gegnerischen, im Zeitablauf koordinieren und bewerten.
6.2. Schach fördert die kreative Problemlösung
Die Redewendung „Viele Wege führen nach Rom“ hat auch in den Naturwissenschaften und im Schach ihre Berechtigung. Die im Spielverlauf entstehenden Schachstellungen können oft auch mit einer anderen Reihenfolge von Schachzügen erreicht werden.
Beispiel (s. Schachdiagramm):
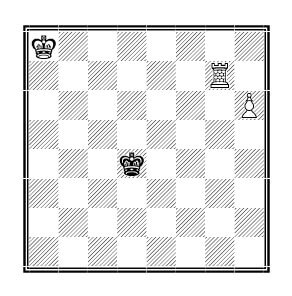
Statt in einem Endspiel (König, Turm und Bauer gegen König) den gegnerischen König mit den vereinten Kräften von König und Turm mattzusetzen, kann zunächst der Bauer in eine andere Figur umgewandelt werden und beide Figuren setzen gemeinsam den gegnerischen König matt.
Es leuchtet prinzipiell ein, dass es leichter ist, mit Dame und Turm zusammen mattzusetzen. Eine Garantie für den Sieg ist es dennoch nicht. Vor allem Anfänger übersehen das Patt-Motiv, d.h., der gegnerische König steht nicht im Schach und hat auch keine Möglichkeit, einen legalen Zug auszuführen. Bei Patt endet die Partie unentschieden, die stärkere Partei hat einen halben Punkt an den Gegner verschenkt. Um nicht in eine Pattfalle zu laufen, muss jeder Schachzug vor dem Ausführen gewissenhaft kontrolliert werden, d.h. die Lage auf dem Schachbrett wird analysiert, um Pattmöglichkeiten rechtzeitig zu erkennen und aus dem Weg zu gehen. Im obigen Beispiel führt das Erkennen des Musters „Treppenmatt“ zum schnellen Erfolg. Bei konsequenter Umsetzung des Gewinnverfahrens Treppenmatt gibt es auch keine Gefahr, dass der Schwarze wegen Patt einen halben Punkt „geschenkt“ bekommt. In Zeitnotphasen der Schachpartie können vermeintlich umständliche Gewinnwege sinnvoll sein, weil der Spieler die Züge routiniert und damit ohne Zeitverlust für zusätzliche Überlegungen und Kontrollen ausführt.
Und diese Erfahrung, aus mehreren zum Ziel führenden Lösungswegen auszusuchen, wird im Schulunterricht oft genug verhindert. Es gibt Mathematiklehrer, die nur einen Lösungsweg als richtig anerkennen und zwar den, den er im Unterricht erklärt hat. Schüler werden in diesem Fällen ausgebremst, Kreativität wird eingeschränkt, Unlust macht sich breit. Die vom Lehrer vorgeführte Methode, wie die Aufgabe gelöst wird, muss nicht die schnellste, einfachste oder für den Schüler verständlichste Methode sein. Es wird erinnert, dass es unzählige Rechenverfahren gibt, wie man mehrstellige Zahlen miteinander addiert oder multipliziert.[64]
Das Anbieten und Erlauben unterschiedlicher Rechenwege zum Lösen der Aufgaben in Mathematik und in den anderen Naturwissenschaften lädt die Schüler zum Mitmachen und Nachdenken ein. Ist der Dreisatz wirklich ein einfaches und verständliches Rechenverfahren? Oder ist ein anderes Rechenverfahren wie die Relationsgleichung mit Darstellung in Bruchschreibweise universeller, einfache und verständlicher? Welche Methode eignet sich für das Rechnen im Kopf besser? (vgl. Anhang B)
Bei den Schach-Anfängern ist zu beobachten, dass zunächst Wunschdenken vorherrscht. Es wird gehofft, dass der Gegner den offensichtlich schlechtesten Zug macht, der zum Partieverlust führt. Dieses Hoffen auf den glücklichen Umstand, dass der Gegner einen groben Schnitzer macht, weicht mit zunehmender Spielerfahrung der Erkenntnis, dass die eigene Zugauswahl auf analytischen Erwägungen erfolgreicher ist. Es wird immer stärker bewusst nach den besten Zügen für beide Seiten Ausschau gehalten. Mit anderen Worten, man muss zu sich ehrlich sein und selbstkritisch denken, wenn man die Schachpartie siegreich gestalten will. Dabei bringt man dem Gegner innerlich Respekt entgegen. intuitiv macht sich der Spieler mit dem dialektischen Prinzip „Ursache und Wirkung“ vertraut, wenn er im Geiste die Zugmöglichkeiten durchgeht und abwägt, welcher Schachzug ihm den größten Nutzen bringen könnte. Die eben beschriebenen Einsichten helfen den Kindern, die oben erwähnte Aufgabe zur Wahrscheinlichkeitsrechnung (verschiedenfarbige Kugeln in einer Kiste) besser zu erfassen und selbständig die richtige Lösung zu finden.
Neben dem selbstkritischen Denken lernen die Kinder, Verantwortung zu übernehmen. Egal wie die Partie endet, der Spieler trägt die Verantwortung für den Erfolg oder Misserfolg. Es gibt keine Ausreden wie:
- der Gegner war wegen Rückenwindunterstützung im Vorteil,
- der Boden war matschig
- hatte keine Möglichkeit einzugreifen (im Fußball oder Handball: weil ihm der Ball nicht zugespielt wurde)
- weil der Gegner ihn foulte
Die Kinder, die Schach lernen, erleben, dass Aufmerksamkeit und zusätzliches Beschäftigen mit Schach zu mehr siegreichen Partien führen. Sie werden für ihren Fleiß mit Erfolgserlebnissen belohnt. Das stärkt das Selbstvertrauen in die eigenen Fähigkeiten und führt zu positiven Veränderungen bei der Einstellung zum Lernen. Schach fördert die Lernmotivation.
Erfahrene Schachtrainer wissen, dass auf dem realen Schachbrett nachgespielte Partien sich besser gemerkt werden als die am Computer nachgespielten Partien. Die eigene Aktivität – das Ziehen der Schachfigur auf dem Schachbrett – ist beim genauen Hinsehen ein komplexer Prozess, vergleichbar mit dem des Schreibens.
Es gibt neben dem klassischen Schach noch viele andere Arten des Schachspielens, die Kindern viel Freude bereiten – wie Schlagschach oder Tandem-Schach. Beim Tandem-Schach, spielen zwei Teams, bestehend aus 2 Spielern, an 2 Schachbrettern. Die beiden Spieler eines Teams spielen mit entgegengesetzten Farben. Jeder Spieler spielt an seinem Brett gegen einen direkten Brettgegner. Die Besonderheit besteht darin, dass die geschlagene Figur an den Teampartner weitergegeben wird, der diese dann entsprechend zuvor vereinbarter Regeln auf dem Schachbrett einsetzen darf. Ein Team hat gewonnen, wenn ein Spieler den Gegner auf seinem Brett mattgesetzt hat. Um erfolgreich zu sein, müssen die Spieler im Team eine gemeinsame Strategie aushandeln und umsetzen. Die gewählte Strategie muss regelmäßig an das tatsächliche Spielgeschehen auf den beiden Schachbrettern angepasst werden, d.h. man muss flexibel reagieren, Kompromisse mit sich und seinem Partner eingehen und als Team harmonisch agieren. Zeit wird eine zusätzliche Dimension, denn ein Abwarten bei einer Partie, bedeutet, dem gegnerischen Team keine Figuren aus einem Abtausch (Schlagen von Figuren) zu liefern, die dann zum Angriff oder Verteidigung eingesetzt werden können.
Auch wenn nicht alle Auswirkungen des Schachs auf Persönlichkeitsmerkmale und Lernerfolg hier beschrieben und erwähnt wurden, so hilft diese Darstellung zu erahnen und zu erfassen, welch gewaltiges lerndidaktisches Instrument das Schachspiel ist.
Mit diesem Wissen versteht man besser, warum sich mehr schachspielende Kinder als nicht schachspielende Kinder für MINT-Berufe interessieren.[65] Eine Auswahl wissenschaftlicher Studien, wie sich Schachunterricht auf Mathematik, Deutsch und verschiedene Persönlichkeitsmerkmale auswirkt, sind im Anhang A angegeben.
In der Broschüre „Schach ein Tool für Bildung und Gesundheit“ (Link) werden noch mehr Auswirkungen des Schachs auf die Persönlichkeitsentwicklung genannt. Die Broschüre gibt es in verschiedenen Sprachen.
Es gibt unzählige Ideen und wissenschaftliche Studien, wie Schach im Schulunterricht und in verschiedenen Fächern außerhalb der Mathematikstunde eingesetzt werden kann. Eine Übersicht gibt es im Internet Link.
Wie in den Studien immer wieder nachgelesen werden kann, bereitet das Schachspiel den Kindern viel Freude. Schach ist nicht nur ernst, sondern auch heiter. Seit jeher gab es Künstler, Dichter und Schriftsteller, die sich mit Schach auseinandersetzen. Es entstanden humorvolle Gedichte, Romane, Filme, Comics, Cartoons und Bilder.
7. Mit dem lerndidaktischen Spiel „Schach“ kostengünstig zu mehr Lernerfolg in der Schule
Schach ist eine kostengünstige und effektive Ressource zur Aktivierung der geistigen Aktivität. Schulen mit Schachspielen auszustatten ist nicht sehr teuer. Bei sorgsamen Umgang mit den Schachbrettern und Schachfiguren besteht für lange Zeit kein Ersatzbedarf. Großfeldschach auf dem Schulhof bietet in den Pausen eine sinnvolle Beschäftigung, fördert die Kommunikation zwischen den Schülern und sorgt für Entspannung. Lehrer und Horterzieher berichten, dass Schach aggressives Verhalten einschränkt.
Die positive Wirkung von Schach auf die schulischen Leistungen bringt der Gesellschaft Vorteile. Der monetäre Wert wurde erstmals 2021 in Dänemark berechnet. „DAMVAD Analytics“, ein dänisches Beratungsunternehmen für fortschrittliche Analysen und Künstliche Intelligenz errechnete einen volkswirtschaftlichen Nutzen in Höhe von ca. 134 Millionen Euro in fünf Jahren[66], wenn alle Kinder regelmäßig Schachunterricht haben. Der sozioökonomische Gewinn resultiert aus den oben beschriebenen positiven Auswirkungen des Schachspiels auf die Persönlichkeitsentwicklung und den Lernerfolg. Bessere Leistungen im Mathematikunterricht geht mit weniger Schulabbrüchen, weniger Straffälligkeiten, besseren Berufsaussichten und in der Folge höheres Einkommen einher. Eingesparte Aufwendungen im Gesundheitsbereich sind schwerer zu quantifizieren.
In die Betrachtung wurde die Entwicklung und Verwendung von Lern-Hilfsmitteln nicht einbezogen. Wie ökonomisch ist es, für die vielen bekannten Lernprobleme individuelle Hilfsmittel (lerndidaktische Spiele, Arbeitshefte, Therapien, …) zu entwickeln? Solche sinnvollen Hilfsmittel, die oft für bestimmte Lernprobleme entwickelt werden, sollten folgenden Anforderungen genügen:
- einfach genug, um ohne neue Hürden aufzubauen, die Hilfsmittel nutzen zu können,
- leicht verfügbar, um sie überall anwenden zu können,
- einfach in der Handhabung, dass unterschiedliche Personen damit arbeiten können (Nicht nur ausgebildete Fachkräfte, sondern auch Eltern, Kinder, Trainer können die Rolle des Therapeuten übernehmen.)
- große Erfolgsaussichten, die gewollten Lernziele zu erreichen (was für jedes Hilfsmittel analog zu neuen Medizinprodukten erst in aufwendigen Studien nachgewiesen werden müsste)
- Hilfsmittel soll den Lernenden nicht stigmatisieren, weil er eine „Sonderbehandlung“ mittels speziellen Hilfsmitteln erhält. Das kann sich negativ auf das Selbstbild, Motivation und Lernergebnis auswirken, abgesehen von möglichen psychischen Problemen, weil er sich „abgestempelt“, als ein vielleicht minderwertiger Mensch fühlt.
- Die Verwendung der Hilfsmittel macht Freude, weil sich das positiv auf die Motivation auswirkt, das Hilfsmittel wiederholt und selbständig zu verwenden
- Kostengünstig, um vielen helfen zu können
Zusammenfassend kann festgestellt werden: Schach ist kein Wundermittel, dass alle Probleme lösen wird. Schach ist vielmehr ein mächtiges, universell wirkendes lerndidaktisches Instrument, was erstaunliche Ergebnisse für breite Schülergruppen bewirken kann. Die Pädagogen müssen keine hervorragenden Schachspieler sein, um Schach im Unterricht einzusetzen. Das spielerische Element vom Schach steht im Vordergrund. Die Pädagogen leiten die Kinder durch die Schachstunde. Es gibt weltweit eine Unmenge an Schachliteratur, die bei der Unterrichtsplanung und –umsetzung direkt verwendet werden kann. Schachprogramme können ebenfalls eingesetzt werden. Sie erklären anschaulich und kindgerecht die Schachregeln und bieten unterhaltsame Übungen an. Die Kinder können selbstständig in ihrem Tempo das Schachspiel erlernen. In jeder Unterrichtstunde sollten die Kinder miteinander Schach spielen. Dabei können sie das Gelernte ausprobieren und anwenden. Wichtig ist, dass die Kinder sich auf die Schachunterrichtsstunde freuen. Dann werden sich über die Zeit positive Effekte einstellen, die die Wissenschaftler in vielen Studien nachgewiesen haben.
Die Argumente für die Aufnahme des Schachspiels in die Lehrpläne der Schulen beruhen in der Regel auf den Vorteilen für die Verbesserung der mathematischen Fähigkeiten. Aber das ist nicht der einzige Vorteil von Schach. Das Schachspiel ist ein Paradebeispiel für eine interdisziplinäre Tätigkeit. Der Schachunterricht an deutschen Schulen würde die Kinder dazu erziehen, die Zusammenhänge mit allen anderen Schulfächern zu erkennen. Es würde sie herausfordern, ihren Verstand – und ja, auch ihren Körper – einzusetzen, um zu lernen, sich zu messen und Spaß zu haben. (in Anlehnung an Prof. Michael Hickson, Universität Trent, Kanada)[67]
weitere Informationen zu den Vorteilen von Schach in der Schule:
Schach – die Schatzkiste der Bildungspolitiker (update zum Beitrag vom 05.02.2022) – Link
Schulschach ist eine enorme sozioökonomische Ressource mit immensen finanziellen Vorteil für die Gesellschaft (05.02.2022) – Link
Zusammenhang zwischen Arbeitsgedächtnis, Lernerfolg und Schach – der Weg zu mehr Lernerfolg – Link
Möglichkeiten, Schach in der Arbeit des pädagogischen Psychologen im Bereich der Bildung einzusetzen – Link
Jerry Nash: „Schach kann die Beziehung zwischen Schülern und Lehrern verbessern“ – Link zu chessbase.de
Lesenswerte Details zu Antworten auf den Brandbrief 2017, der Mathematikdefizite von Studienanfängern beklagte (mit Aufgabenbeispielen, 2018) – Link
Referenzen
[1] Benjamin Franklin (1706 1790) – amerikanischer Schriftsteller, Naturwissenschaftler und Staatsmann
[2] Kollosche, D. (2018). Soziale Dimensionen der Wahrnehmung von Mathematik durch Schüler. In: Nickel, G., Helmerich, M., Krömer, R., Lengnink, K., Rathgeb, M. (eds) Mathematik und Gesellschaft. Springer Spektrum, Wiesbaden. https://doi.org/10.1007/978-3-658-16123-1_22
[3] IQB-Bildungstrends 2021, Seite 54
[4] IQB-Bildungstrends 2021, Seite 55
[5] 17.10.2022 „KMK stellt sich neuesten Befunden des IQB-Bildungstrends: Gezielte Maßnahmen zur Sicherung der Mindeststandards sind notwendig“, URL: https://www.kmk.org/aktuelles/artikelansicht/kmk-stellt-sich-neuesten-befunden-des-iqb-bildungstrends-gezielte-massnahmen-zur-sicherung-der-minde.html
[7] Nationaler PISA-Bericht 2018, Seite 204 ff.
[8] Spiegel online, Zahl der Schulabgänger ohne Abschluss steigt (2020) URL: https://www.spiegel.de/panorama/bildung/bildungsbericht-des-bundes-zahl-der-schulabgaenger-ohne-abschluss-steigt-a-d856b93b-f851-4266-be73-22982af83dfe
[9] 2019, Bildungsstandards im Schulfach Mathematik, Brief an die die Kultusministerkonferenz https://angewandte-didaktik.mathematik.uni-mainz.de/files/2020/03/Brief-KMK-20190815-Bildungsstandards.pdf
[10] Hafner, T. (2012). Proportionalität und Prozentrechnung in der Sekundarstufe I. Empirische Untersuchung und didaktische Analysen (Dissertation). Wiesbaden: Vieweg+Teubner
[11] Gudladt, P. (2021). Didaktische Überlegungen. In: Inhaltliche Zugänge zu Anteilsvergleichen im Kontext des Prozentbegriffs. Perspektiven der Mathematikdidaktik. Springer Spektrum, Wiesbaden. https://doi.org/10.1007/978-3-658-32447-6_2
[12] Die Gartenlaube (1890). Ernst Keil’s Nachfolger, Leipzig 1890, Seite 548. Digitale Volltext-Ausgabe bei Wikisource, URL: https://de.wikisource.org/w/index.php?title=Seite:Die_Gartenlaube_(1890)_548.jpg&oldid= – (Version vom 20.1.2023)
[13] Spektrum der Wissenschaft, 10.10.2013, Rechenschwäche gibt es nicht, URL: https://www.spektrum.de/news/rechenschwaeche-gibt-es-nicht/1209908
[14] Gaidoschik, Michael & Moser Opitz, Elisabeth & Nührenbörger, Marcus & Rathgeb-Schnierer, Elisabeth & Götze, Daniela. (2021). Besondere Schwierigkeiten beim Mathematiklernen. 10.13140/RG.2.2.15952.64004., URL: https://www.zebis.ch/unterrichtsmaterial/besondere-schwierigkeiten-beim-mathematiklernen
[15] Gaidoschik, Michael & Moser Opitz, Elisabeth & Nührenbörger, Marcus & Rathgeb-Schnierer, Elisabeth & Götze, Daniela. (2021). Besondere Schwierigkeiten beim Mathematiklernen. 10.13140/RG.2.2.15952.64004., URL: https://www.zebis.ch/unterrichtsmaterial/besondere-schwierigkeiten-beim-mathematiklernen
[16] Schulze, Sarah & Kuhl, Jan. (2018). Integration von Arbeitsgedächtnistrainings in die mathematische Lernförderung. Lernen und Lernstörungen 8 (1) Link
[17] Psychologie für den Lehrberuf Urhahne, D., Dresel, M., Fischer, F. 2019, XVI, 636 S. Mit Online-Extras, Hardcover ISBN: 978-3-662-55753-2, 28, URL: https://lehrbuch-psychologie.springer.com/sites/default/files/atoms/files/urhahne_a1_978-3-662-55753-2_leseprobe_1.pdf
[18] Viesel-Nordmeyer, N., Ritterfeld, U. & Bos, W. Welche Entwicklungszusammenhänge zwischen Sprache, Mathematik und Arbeitsgedächtnis modulieren den Einfluss sprachlicher Kompetenzen auf mathematisches Lernen im (Vor‑)Schulalter?. J Math Didakt 41, 125–155 (2020). https://doi.org/10.1007/s13138-020-00165-0
[19] Stegariu, Vlad-Ionut, and Beatrice Abalasei. „Correlation between Attentional Abilities and Spatial Orientation in Children Who Study Chess in School.“ Revista Romaneasca pentru Educatie Multidimensionala 14.3 (2022): 126-138. URL: https://www.lumenpublishing.com/journals/index.php/rrem/article/download/5267/3910
[20] Winkelmann, Jan, Mareike Freese, and Tim Strömmer. „Schwierigkeitserzeugende Merkmale im Physikunterricht: Die Perspektive von Schüler* innen.“ Progress in Science Education (PriSE) 5.2 (2022): 6-23. URL: https://e-publishing.cern.ch/index.php/prise/article/download/1168/1112/5559
[21] Richard Feynman (1918-1988) – amerikanischer Physiker und Nobelpreisträger
[22] Lin-Siegler, X., Ahn, J. N., Chen, J., Fang, F. F. A., & Luna-Lucero, M. (2016). Even Einstein struggled: Effects of learning about great scientists’ struggles on high school students’ motivation to learn science. Journal of Educational Psychology, 108(3), 314, URL: https://psycnet.apa.org/manuscript/2016-07217-001.pdf
[23] Siehe Fußnote 18 (Lin-Sigler)
[24] SWR2, 28.10.2022 , URL: https://www.swr.de/swr2/wissen/problemfach-mathe-wie-schule-fuer-zahlen-und-logik-begeistern-koennte-swr2-wissen-2022-10-29-100.html
[25] IQB-Bildungstrends 2018, Seite 372
[26] IQB-Bildungstrends 2018, Seite 447
[27] Fischer, Marc; Irgl, Christian. “ Mit den Tiefenstrukturen wird der Blick stärker auf die Schüler*innen und auf ihre Lernprozesse gerichtet.“ Das Heft-Pädagogische Hochschule FHNW. (2020) 4. URL: Link
[28] Yu, Qinmei, Stella Patino, and Tracy Harris. „Creating Joyful “Third Space” for Young Dual Language Learners via Family-involved Chess Playing Project.“ Journal of Education and Human Development 9.4 (2020): 108-116.
URL: http://jehdnet.com/journals/jehd/Vol_9_No_4_December_2020/11.pdf
[29] In englisch: „What humans do with the language of mathematics is describe patterns.“ (Steen, 1990), Lynn Arthur Steen – amerikanischer Mathematiker und Mathematikpädagoge
[30] Koerber, S., Mayer, D., Osterhaus, C., Schwippert, K. and Sodian, B. (2015), The Development of Scientific Thin-king in Elementary School: A Comprehensive Inventory. Child Dev, 86: 327-336. https://doi.org/10.1111/cdev.12298
[31] Steen, Lynn Arthur. „Reflections on Mathematical Patterns, Relationships, and Functions.“ Prepared for the Minnesota K-12 Mathematics Framework, SciMath-MN (1998). URL: http://www.steen-frost.org/Steen/Papers/98algebra_mn.pdf
[32] Ch, Erich & Wittmann,. (2005). Mathematics as the science of patterns–a guideline for developing mathematics education from early childhood to adulthood. Link
[33] Vogel, R. Muster – eine Grundidee des mathematischen Denkens und Lernens. ZDM 37 , 445–449 (2005). https://doi.org/10.1007/s11858-005-0035-z
[34] Maries, Alexandru, and Chandralekha Singh. „Helping Students Become Proficient Problem Solvers Part I: A Brief Review.“ Education Sciences 13.2 (2023): 156., URL: https://www.mdpi.com/2227-7102/13/2/156
[35] Bilalić, Merim, et al. „Mechanisms and neural basis of object and pattern recognition: a study with chess experts.“ Journal of Experimental Psychology: General 139.4 (2010): 728. URL: https://cognition.aau.at/download/Publikationen/Bilalic/Bilalic_etal_2010a.pdf
[36] John F. Kennedy (1917 – 1963) – 35. Präsident der USA
[37] Spitzer, Manfred. „Keilschrift, Kant und Kaufverträge.“ Nervenheilkunde 39.04 (2020): 198-205. URL: https://www.thieme-connect.com/products/ejournals/html/10.1055/a-1033-9748
[38] Buddeberg, Magdalena, and Anke Hußmann. „Kapitel I Verlängerte Unterrichtsstunden aus Sicht von Lehrkräften sowie Schülerinnen und Schülern.“ Mareike Haas und Maria Krieg (Hg.) (2021): 15-28. URL: Link
[39] Haunhorst, D., Hüfner, C., Kastrup, V., Mergelkuhl, T., Röllke, K., & Wilde, M. (2022). Sport und Biologie fächerübergreifend unterrichten : Die Planung und Umsetzung fächerübergreifender Unterrichtskonzepte im Rahmen eines universitär begleiteten Schulpraktikums. Herausforderung Lehrer*innenbildung – Zeitschrift Zur Konzeption, Gestaltung Und Diskussion, 5(1), 26–42. https://doi.org/10.11576/hlz-5152
[40] Kramer, N., & Wegner, C. (2020). Fächerübergreifender Unterricht im Fächerverbund Naturwissenschaften und Sport: Darstellung eines systematischen Reviews. Herausforderung Lehrer*innenbildung – Zeitschrift Zur Konzeption, Gestaltung Und Diskussion, 3(1), 689–715. https://doi.org/10.4119/hlz-2544
[41] Blanch, A. Chess Instruction Improves Cognitive Abilities and Academic Performance: Real Effects or Wishful Thinking?. Educ Psychol Rev 34, 1371–1398 (2022). https://doi.org/10.1007/s10648-022-09670-9
[42] Blanch, A. Chess Instruction Improves Cognitive Abilities and Academic Performance: Real Effects or Wishful Thinking?. Educ Psychol Rev 34, 1371–1398 (2022). https://doi.org/10.1007/s10648-022-09670-9
[43] siehe Fußnote 36
[44] Tyler W. Watts, Drew H. Bailey & Chen Li (2019) Aiming Further: Addressing the Need for High-Quality Longitudinal Research in Education, Journal of Research on Educational Effectiveness, 12:4, 648-658, https://doi.org/10.1080/19345747.2019.1644692
[45] Direkter Link zur Tabelle URL: https://link.springer.com/article/10.1007/s10648-022-09670-9/tables/2
[46] Zaretskiy V. K., CHESS FOR GENERAL DEVELOPMENT: REFLECTIVE AND ACTIVITY APPROACH TO CORRECTING BEHAVIORAL DISORDERS (2018), URL: https://www.mental-health-congress.ru/media/document/final_document/29/СБОРНИК%20НАУЧНЫХ%20СТАТЕЙ.pdf
[47] In Englisch: „One step in learning may mean one hundred steps in development.“ Und in Russisch: „Один шаг в обучении может означать сто шагов в развитии.“
[48] Zaretskiy V. K., Glukhova O. V. “ The reflexive activity approach to teaching chess at school: Satka experience“ II International Conference on Consultative Psychology and Psychotherapy dedicated to the memory of F.E. Vasilyuk: collection, no. 1, 2020, pp. 100-104. https://doi.org/10.24411/9999-055A-2020-00023
[49] in Englisch „abiltiy to act in the mind“ und in Russisch „способность действовать в уме“, weitere Informationen:
Zak A.Z. CHARACTERISTICS OF THE ABILITY TO ACT „IN THE MIND“ OF FIRST-GRADERS // Международный журнал гуманитарных и естественных наук. 2022. №10-2. URL: https://cyberleninka.ru/article/n/characteristics-of-the-ability-to-act-in-the-mind-of-first-graders
[50] Barma, S. & Zaretskii, Z. K. (2017), Contemporary Russian Contributions to Vygotsky’s Heritage. Special Issue. CRI_SAS International Journal/Revue internationale du CRIRES: innover dans la tradition de Vygotsky, 4(1). ISSN:2291–6717, URL: https://revues.ulaval.ca/ojs/index.php/RIC/issue/view/22
[51] Glukhova O.V., Volikova S.V., Zaretsky Y.V., Zaretsky V.K. The Results of a Longitudinal Diagnostic Study on the Project «Chess for Overall Development». Konsul’tativnaya psikhologiya i psikhoterapiya = Counseling Psychology and Psychotherapy, 2022. Vol. 30, no. 4, pp. 49–75. URL: https://doi.org/10.17759/cpp.2022300404 . (In Russ., аbstr. in Engl.)
[52] „chess universal“ wurde von Igor Sukhin entwickelt. Er arbeitet in leitender Funktion am Institut der Strategie der Bildungsentwicklung der Russischen Akademie der Wissenschaften in Moskau.
[53] Romanova, I., Vasylieva M., Podberezskyi.M. „Chess therapy as a new trend in training of future social pedagogues.“ (2018). URL: http://efsupit.ro/images/stories/october2018/Art%20266.pdf
[54] Panagiotidi, M., Overton, P. Aufmerksamkeitsdefizit-Hyperaktivitätssymptome sagen eine problematische Mobiltelefonnutzung voraus. Curr Psychol 41 , 2765–2771 (2022). https://doi.org/10.1007/s12144-020-00785-2
[55] Veloso A, Vicente SG and Filipe MG (2020) Effectiveness of Cognitive Training for School-Aged Children and Adolescents With Attention Deficit/Hyperactivity Disorder: A Systematic Review. Front. Psychol. 10:2983. URL: https://doi.org/10.3389/fpsyg.2019.02983
[56] Yanguas, María Rodrigo. Efectividad de una aplicación informática personalizada basada en el ajedrez para el tratamiento de niños y adolescentes con trastorno de déficit de atención con hiperactividad (TDAH): Un ensayo clínico. Diss. Universidad Autónoma de Madrid, 2021.
[57] Scholz, Markus, et al. „Impact of Chess Training on Mathematics Performance and Concentration Ability of Children with Learning Disabilities.“ International Journal of Special Education 23.3 (2008): 138-148. URL: https://files.eric.ed.gov/fulltext/EJ833690.pdf
[58] URL: https://www.zeit.de/2022/33/jarno-scheffner-schach-amateur-weltmeister
[59] Sidorenko A.A. Teaching Chess on the Basis of the Refletiive-Activity Approach in the Context of the Problem of Gaining Legal Capacity: a Case from Practice. Konsul’tativnaya psikhologiya i psikhoterapiya = Counseling Psychology and Psychotherapy, 2022. Vol. 30, no. 4, pp. 76–96. https://doi.org/10.17759/cpp.2022300405 (In Russ., аbstr. in Engl.)
[60] AlphaZero ist ein autodidaktisches Computerprogramm von DeepMind, dessen Algorithmus mehrere komplexe Brettspiele einzig anhand der Spielregeln und Siegbedingungen sowie durch intensives Spielen gegen sich selbst erlernt. (Wikipedia)
[61] Franklin, James. „Mathematics as a science of non-abstract reality: Aristotelian realist philosophies of mathematics.“ Foundations of Science 27.2 (2022): 327-344, URL: https://philpapers.org/archive/FRAMAA-12.pdf
[62] Kreutzer, R.T. (2020). Mangelnde Konzentrationsfähigkeit. In: Die digitale Verführung. Springer, Wiesbaden. https://doi.org/10.1007/978-3-658-27781-9_2
[63] John, D.T., Wieland, U., Blickhan, D. (2019). Achtsamkeitsinterventionen in der Schule. In: Chang-Gusko, YS., Heße-Husain, J., Cassens, M., Meßtorff, C. (eds) Achtsamkeit in Arbeitswelten. FOM-Edition. Springer Gabler, Wiesbaden. https://doi.org/10.1007/978-3-658-25673-9_11
[64] Miller, Maximilian „Rechenvorteile“. BSB B.G. Teubner Verlagsgesellschaft Leipzig. (1963)
[65] Zlabinger, Florian. Mathematik und Schach: Ansichten schachspielender Kinder und Jugendlicher zum Themengebiet Mathematik/eingereicht von Florian Zlabinger, BSc. Diss. Universität Linz, 2021. URL: https://epub.jku.at/obvulihs/content/titleinfo/5884149/full.pdf
[66] „En times skoleskak om ugen giver en stor samfundsøkonomisk gevinst“, https://www.danskindustri.dk/lad-os-lose-det-sammen/cases/cases/damvad-analytics-x-dansk-skoleskak/ (Dezember 2021)
[67] Michael Hickson, „Why Canada should invest more in teaching kids how to play chess“. The Conversation. (13.10.2022) URL: https://theconversation.com/why-canada-should-invest-more-in-teaching-kids-how-to-play-chess-191413
Anhang A Übersicht wissenschaftlicher Arbeiten zu Schach in der Schule
Tabellen in Anlehnung an: Ortiz-Pulido, Ricardo, et al. „Neuroscientific evidence support that chess improves academic performance in school.“ Revista mexicana de neurociencia 20.4 (2019): 194-199. URL: https://www.medigraphic.com/pdfs/revmexneu/rmn-2019/rmn194e.pdf
Tabelle 1
Einige Studien, in denen festgestellt wurde, dass Schach die mathematischen Leistungen in der Schule beeinflusst
| Autor(en) | Land | N | Studienziel | Tests | Ergebnisse |
| Fernandez-Amigo et al.
T1 (Jahr 2008) |
Spanien | N = 141 Versuchsgruppe (79 Jungen, 62 Mädchen) | Qualitative und quantitative Analyse des Nutzens von schachbasierten Unterrichtsmaterialien für den Mathematikunterricht in der zweiten Klasse der Grundschule | EFAI (Factorial Evaluation of Intellectual Aptitudes) Numerische Punktzahl, Punktzahl für logisches Denken, ethnographisches Interview, Umfragen | Zufriedenheit mit dem Einsatz des schachbasierten Lernmaterials für den Mathematikunterricht |
| Achig und Francisco
T2 (Jahr 2015) |
Ecuador | N = 35 Versuchsgruppe (20 Jungen, 15 Mädchen) | Prüfung der Auswirkungen des Schachspiels auf das logisch-mathematische Denken von Schülern der sechsten Klasse | Theoretischer Schachtest vorher und nachher, Note
im Mathematikunterricht |
Die Durchschnittsnote im Mathematik-unterricht stieg |
| Guerrero et al.
T3 (Jahr 2015) |
Mexiko | N = 32 Die Anzahl Jungen gegenüber Mädchen wird nicht angegeben | Beschreibung der Auswirkungen des Schachspiels auf die Grundrechenarten von Schülern der fünften Klasse | Pretest und Posttest zu Brüchen und Operationen basierend auf ENLACE 2011 und 2012 Testfragen, Umfragen und Interviews | Bessere Konzentration, besseres Gedächtnis und bessere Noten im Mathematikunterricht |
| Gumede und Rosholm
T4 (Jahr 2015) |
Dänemark | N = 264 Die Anzahl Jungen gegenüber Mädchen wird nicht angegeben | Charakterisierung der Auswirkungen von Schach im Fach Mathematik bei Grundschülern der ersten und dritten Klasse | Tests vor der Intervention, persönliche Merkmale des Kindes sowie der Mutter und des Vaters des Kindes | Positive Auswirkungen sowohl bei dänischen Kindern mit als auch ohne Migrationshintergrund |
| Sala et al
T5 (Jahr 2015) |
Italien | N = 309 Versuchsgruppe (169 Jungen, 140 Mädchen). N = 251 Kontrollgruppe (116 Jungen, 135 Mädchen). |
Untersuchung des Potenzials von Online-Schachunterricht auf die Problemlösungsfähigkeiten von Grundschülern der zweiten, vierten und fünften Klasse | PISA und Schachumfrage | Starke positive Korrelation zwischen Mathe und Schach in der Versuchsgruppe |
| Sala et al
T6 (Jahr 2016) |
Italien | N = 309 Versuchsgruppe (169 Jungen, 140 Mädchen) N = 251 Kontrollgruppe (116 Jungen, 135 Mädchen) |
Experimentelle Studie über Schach bei Grundschülern der vierten Klasse mit einer Placebogruppe | Sechs Tests zur Bewertung der mathematischen Fähigkeiten, IEA – TIMSS psychometrischer Test | Die Schachgruppe war in den mathematischen Fähigkeiten effektiver als die GO-Gruppe, aber nicht in den schulischen Aktivitäten |
| Rosholm et al.
T7 (Jahr 2017) |
Dänemark | N = 323 Versuchsgruppe.
N = 159 Kontrollgruppe |
Analyse der Auswirkungen des Ersetzens einer Mathematikstunde pro Woche durch einen Schachunterricht für Grundschüler der ersten und dritten Klasse | Mathematik Test (einschließlich Berechnungen, Geometrie, Mustererkennung und grundlegendes Problemlösen) | Verbesserung der Bildung von mathematischen Folgen in der Versuchsgruppe |
| Meloni und Fanari
T8 (Jahr 2019) |
Italien | N = 48 Versuchsgruppe.
N = 37 Kontrollgruppe |
Analyse der Auswirkungen des Ersetzens einer Mathematikstunde pro Woche durch einen Schachunterricht für Grundschüler der ersten und dritten Klasse | Mathematik Test (einschließlich Berechnungen, Geometrie, Mustererkennung und grundlegendes Problemlösen) | Verbesserung der Bildung von mathematischen Folgen in der Versuchsgruppe |
| Tachie und Ramathe
T9 (Jahr 2022) |
Südafrika | N = 25
Versuchsgruppe Kontrollgruppe Die Anzahl Jungen gegenüber Mädchen wird nicht angegeben |
Analyse der Auswirkungen des Ersetzens einer Mathematikstunde pro Woche durch einen Schachunterricht für Schüler der neunten Klasse | Gruppentest | Die Schachgruppe war in den mathematischen Fähigkeiten effektiver |
Tabelle 2
Einige Studien, die den Einfluss von Schach auf das Leseverständnis in der Schule untersuchen
| Autor(en) | Land | Zahl der Teilnehmer | Studienziel | Tests | Ergebnisse |
| Margulies et al
T10 (Jahr 1991) |
USA | N = 1118 Teilnehmergruppen N = 22 | Beschreibung der Auswirkungen auf das Lesen vor und nach dem Schachunterricht in der Grundschule | Test zum Stand der Leseleistung (DRP) | Die Gruppe der Schachschüler verbesserte sich mehr als der durchschnittliche Schüler |
| Liptrap et al
T11 (Jahr 1998) |
USA | N = 571 gesamt Schachgruppe N = 67 Gruppe, die kein Schach gespielt hat N = 504 | Bestimmung des Ausmaßes der Teilnahme von Schülern an einem Schachklub | Texas Assessment of Academic Skills (TAAS). Texas Learning Index (TLI) | Die Schachgruppe verbesserte sich mehr in Mathematik als im Lesen |
| Duccette
T12 (Jahr 2009) |
USA | Versuchsgruppe N = 151 | Analyse der Auswirkungen eines Schachprogramms auf Verhalten, Mathematik und Lesen | Philadelphia’s behavior grade and attendance, Pennsylvania System of school Achievement (PSSA)
Punktzahl in Lesen und Mathematik |
Nach 1 Jahr verbesserte sich die Gruppe, die Schach spielte, in Mathematik und Lesen, und diese Werte waren korreliert, während in der Kontrollgruppe keines dieser Merkmale vorhanden war |
| Dapica Tejada
T13 (Jahr 2016) |
Spanien | N = 60 Gesamt
Schachgruppe N = 30 (21 Jungen, 9 Mädchen) Kontrollgruppe N = 30 (20 Jungen, 10 Mädchen) |
Prüfung, ob es signifikante Unterschiede im Leseverständnis und in den sakkadischen Bewegungen (SM * ) bei Jungen und Mädchen gibt, die Schach spielen | Umfrage zur Teilnahme am Schachspiel, PROLEC-SE Testbatterie für Leseprozesse und King Devick SM-Test | Die Schachgruppe verbesserte sich bei den verschiedenen Tests, bei denen sie bewertet wurde, was bei der Nicht-Schachgruppe nicht der Fall war. Darüber hinaus gab es eine Korrelation zwischen SM und Leseverständnis und zwischen Schach und SM |
| Celiz
T14 (Jahr 2020) |
Peru | N = 56 Gesamt
Schachgruppe N = 27 Kontrollgruppe N = 27 |
Auswirkung des Schachs auf das Leseverständnis bei Grundschülern der dritten Klasse | Pretest und Posttest | Leseverständnis
verbesserte sich |
* SM werden in den Augen erzeugt, wenn wir lesen, schauen oder nach Informatione
Tabelle3
Einige Studien, die den Einfluss von Schach auf Persönlichkeitsmerkmale untersuchen
| Autor(en) | Land | Zahl der Teilnehmer | Studienziel | Tests | Ergebnisse |
| Filipp et al
T15 (Jahr 2007) |
Deutsch-lnad | N = 84
Schachgruppe N = 83 Kontrollgruppe |
Auswirkung von Schach auf die geistige und schulische Entwicklung bei Schülern der ersten bis vierten Klasse, über 3 Jahre | Grundintelligenztest Skala Differentielle Leistungstest
Konzentrationsfähigkeit (TPK) Hamburger Schreib-Probe Fragebogen |
Die Schachgruppe schnitt im Leseverständnis, Arithmetik überdurchschnittlich ab,
Verbesserungen in Einstellungen und sozialverhalten |
| Aciego et al.
T16 (Jahr 2012) |
Spanien | N = 170
Schachgruppe N = 60 Kontrollgruppe |
Auswirkungen des regelmäßigen Schachunterrichts auf intellektuelle und sozio-affektive Fähigkeiten | Leistungstest WISC-R
Selbsteinschätzung TAMAI Pretest und Posttest Fremdevaluation |
Die Schachgruppe verbesserte sich bei kognitiven und sozioaffektiven Fähigkeiten (Selbstbewusstsein, Lernmotivation, Aufmerksamkeit, visuomotorische Koordination,…) |
| Ramos et al
T17 (Jahr 2017) |
Argentinien | N = 65 Gesamt
(42 Jungen, 23 Mädchen) Schachgruppe N = 30 (28 Jungen, 2 Mädchen) Kontrollgruppe N = 35 (14 Jungen, 21 Mädchen) |
Analyse der Unterschiede in der kognitiven Leistung bei Kindern, die Schach üben und Kindern, die kein Schach üben | Ex-Post-Facto Querschnittsstudie
Stroop-Word-Color-Test WISC IV WCST Labyrinth-Test nach Porteus Multivariate Varianzanalyse |
Die Schachgruppe erreicht höhere Werte bei Planung, Arbeitsgedächtnis, kognitive Flexibilität |
| Joseph et al.
T18 (Jahr 2018) |
Indien | Schachgruppe
N = 70 (43 Jungen, 27 Mädchen) Kontrollgruppe N = 81 (52 Jungen, 29 Mädchen) |
Auswirkungen des systematisches Schachtrainings auf das verbale Denken | Pretest und Posttest
ANCOVA Binet–Kamat-Intelligenz-Test |
Nach 2 Jahren signifikante Steigerung der Fähigkeit des sprachlichen Denkens bei der Schachgruppe,
keine Unterschiede zwischen den Geschlechtern |
| Atashafrouz
T19 (Jahr 2019) |
Iran | N = 40 Gesamt
Schachgruppe N = 20 Kontrollgruppe N = 20 |
Auswirkungen von Schach auf die Fähigkeit zur Problemlösung, das Arbeitsgedächtnis und die Konzentration für Schüler der zehnten Klasse | Pretest und Posttest,
Cassidy und Lang’s problem-solving style questionnaire (PSSG), Cornoldi’s working memory test (CWMT) und Weinstein und Palmer’s learning and study strategies inventory (LASSI) |
Die Schachgruppe zeigte deutlich bessere Ergebnisse für Arbeitsgedächtnis und der Konzentration |
| Gündüz et al
T20 (Jahr 2019) |
Türkei | N = 25 Gesamt
Speer Trainees N = 20 Peer Trainers N = 5 |
Auswirkungen des Schachunterrichts als Peer-Learning in den Grundschulklassen | Fragebögen
Peer-Evaluierungs-formulare Befragungen |
Verbesserung der kognitiven Fähigkeiten, der Kommunikation und des Sozialverhaltens |
| Sandoval-Tipán und Ramos-Galarza
T21 (Jahr 2020) |
Ecuador | N = 60 Gesamt
(41 Jungen, 19 Mädchen) Schachgruppe N = 30 Kontrollgruppe N = 30 |
Auswirkungen von Schach auf das Arbeitsgedächtnis und die Planungsfähigkeit bei Grundschülern | ENFEN-Testbatterie,
Labyrinth-Test nach Porteus, Beobachtungsfragebogen |
Die Schachgruppe zeigte deutlich bessere Ergebnisse für Arbeitsgedächtnis und Planungsfähigkeit |
| Tanajyan et al
T22 (Jahr 2021) |
Armenien | N = 264 Gesamt
Verteilung der Schüler nach Klassenstufen Schularten und Geschlecht |
Einstellung zum Schachunterricht und dessen Auswirkungen auf das Sozialverhalten bei Kindern der zweiten bis vierten Klasse | Standardisiertes Interview mit Multiple Choice
Tests – Wertetheorie nach Rokeach |
Überwiegende Mehrheit macht gern Schach,
positive Auswirkung auf Kooperationsverhalten, Motivation, Ehrlichkeit, Planung, Disziplin |
| Gao et al.
T23 (Jahr 2021) |
China | N = 255 Gesamt
Verteilung der Schüler nach Klassenstufen Schularten und Geschlecht |
Beziehungen zwischen Fluid-Intelligenz, Fähigkeiten im Schach und Schulleistungen | Raven’s Standard Progressive Matrices
Befragung Schulprüfungen Multivariate Varianzanalyse |
positiver Zusammenhang zwischen fluider Intelligenz und Schulleistung,
Schachfähigkeiten korrelieren mit schulischen Leistungen |
| Glukhova
T24 (Jahr 2022) |
Russland | 1. Phase
N = 637 Gesamt Schachgruppe 1 N=331 mit Lehrprogramm „chess project“ Schachgruppe 2 N = 160 mit Lehrprogramm „Chess universal“ Kontrollgruppe N = 146 ohne Schachprogramm
über alle Phasen N = 1571 davon N = 723 mit Lehrprogramm „chess project |
Steigerung des Entwicklungsniveaus intellektueller Prozesse bei Kindern mittels Schach auf Basis des Ansatzes der Reflexionsaktivität mit Schülern der ersten bis neunten Klasse über 4 Jahre und Langzeitwirkung,
insgesamt 18 Jahre
|
Test zum Erinnerungsvermögen,
Test zum visuellen Gedächtnis Tests zu Analogien Raven’s Standard Progressive Matrices Correction test Bourdon |
Stabile Verbesserung intellektueller Leistungen,
der Schachgruppen Entwicklungsvorsprung bleibt bis in hohe Schulklassen erhalten |
| Chitiyo et al.
T25 (Jahr 2023) |
USA | N = 1286 Gesamt
Verteilung der Schüler nach Klassenstufen Schularten und Geschlecht |
Unterschiede in den wahrgenommenen Vorteilen von Schach durch die Schüler nach Geschlecht und Alter sowie unterschiedlicher Schulen und Jahrgänge
zu bestimmen Vorteile: Freude, Selbstvertrauen, organisatorische Fähigkeiten, Lernmotivation, Selbstwirksamkeit, Kooperationsfähigkeit, organisatorische fähigkeiten |
Retrospektiver Pretest und Posttest
Multivariate Varianzanalyse |
Lernmotivation bei Grundschülern am höchsten und in allen Klassenstufen bei Mädchen mehr als bei Jungen,
Freude hatten mehr Jungen als Mädchen, die Grundschüler hatten die meiste Freude, Kooperationsfähigkeit verbesserte sich am stärksten bei Grundschülern, Wahrnehmung von Vorteilen ist von Geschlecht und Klassenstufe abhängig |
zu Tabelle 1 (Anhang A)
- Fernández-Amigo J, Gairín Sallán J. Utilización de Material Didáctico con Recursos de Ajedrez Para la Enseñanza de las Matemáticas Barcelona. España: universidad de Barcelona; 2008, URL: https://www.tesisenred.net/handle/10803/5053
- Achig F, Francisco J. Artículo Científico-Incidencia de la Enseñanza del Ajedrez en la Asignatura de Matemáticas en los y las Estudiantes del 6to. año de Educación Básica de la Unidad Educativa Hermano Miguel de la Salle-Cuenca en el Período de Enero a Junio de 2012-2015, URL: http://repositorio.espe.edu.ec/xmlui/handle/21000/7049
- Guerrero SG, Martínez RM, Alonzo MM. EL ajedrez para el aprendizaje de operaciones básicas y números fraccionarios en un grupo de quinto grado de educación primaria. Rev Invest Educ Esc Grad Educ. 2015;6:9-14. URL: https://sibi.upn.mx/cgi-bin/koha/opac-detail.pl?biblionumber=197301
- Gumede K, Rosholm M. Your Move: the Effect of Chess on Mathematics Test Scores. Discussion Paper; 2015 URL: https://docs.iza.org/dp9370.pdf
- Sala G, Gorini A, Pravettoni G. Mathematical problem-solving abilities and chess: an experimental study on young pupils. SAGE Open. 2015;5:2158244015596050 URL: https://doi.org/10.1177/2158244015596050
- Sala G, Gobet F, Trinchero R, Ventura S. Chess instruction enhance mathematical ability in children? A three group design to control for placebo effects. In: does Chess Instruction Enhance Mathematical Ability in Children? Philadelphia, PA: a Three Group Design to Control for Placebo Effects; 2016 URL: https://livrepository.liverpool.ac.uk/3002154/1/sala_cogsci-2016.pdf
- Rosholm M, Mikkelsen MB, Gumede K. Your move: the effect of chess on mathematics test scores. PLoS One. 2017;12:e0177257 URL: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0177257
- Meloni, Carla, and Rachele Fanari. „Chess Training Effect on Meta-Cognitive Processes and Academic Performance.“ International Association for Development of the Information Society; URL: https://doi.org/10.33965/celda2019_201911L048
- Tachie, Simon Adjei, and Johnson Motingoe Ramathe. „Metacognition Application: The Use of Chess as a Strategy to Improve the Teaching and Learning of Mathematics.“ Education Research International2022; 2022 URL: https://doi.org/10.1155/2022/6257414
zu Tabelle 2 (Anhang A)
- Margulies S. The Effect of Chess on Reading Scores. Report. Vol. 10. New York: the American Chess Foundation; 1991. p. 13-25 URL: https://rknights.org/wp-content/uploads/margulies.pdf
- Liptrap JM. Chess and Standard Test Score. London: chess Life; 1998. p. 41-3 URL: https://saintlouischessclub.org/education/research/chess-and-standard-test-scores
- DuCette J. An Evaluation of the Chess Challenge Program of ASAP/After school Activities Partnerships. Philadelphia, PA: after School Activities Parnerships; 2009. p. 1-13 URL: http://il-chess.org/non_joom/youthpdfs/BradASAPsummary.pdf
- Dapica-Tejada R. Influencia del Ajedrez en la Comprensión Lectora y los Movimientos Sacádicos en Niños Madrid. España: universidad Internacional de la Rioja; 2016 URL: https://reunir.unir.net/handle/123456789/4371
- Mamani Celiz, Edwin. La enseñanza del ajedrez para la comprensión lectora en estudiantes de primaria de la unidad educativa “Kalajawira” de la ciudad de La Paz, gestión 2019. Diss. 2020. URL: https://repositorio.umsa.bo/handle/123456789/24961
zu Tabelle 3 (Anhang A)
- Filipp, Sigrun-Heide, and H. Spieles. „Fördert Schachunterricht in der Grundschule die geistige Entwicklung der Kinder.“ Abschlussbericht über eine Evaluationsstudie zum Schachunterricht in einer Trierer Grundschule. Trier: ZDiag(2007). URL: https://nsv-online.de/downloads/Endbericht-Abschlusskorrektur13-02-07.pdf
- Aciego, Ramón, Lorena García, and Moisés Betancort. „The benefits of chess for the intellectual and social-emotional enrichment in schoolchildren.“ The Spanish journal of psychology2 (2012): 551-559. URL: http://chessedu.org/wp-content/uploads/social-emotional-benefits-1.pdf
- Ramos, Larisa, Vanessa Arán Filippetti, and Gabriela Krumm. „Funciones ejecutivas y práctica de ajedrez: un estudio en niños escolarizados.“ Psicogente39 (2018): 25-34. URL: http://www.scielo.org.co/pdf/psico/v21n39/0124-0137-psico-21-39-00025.pdf
- Joseph, Ebenezer, et al. „Enhancing verbal reasoning of school children through chess learning.“ International Journal of Scientific Engineering and Science7 (2018): 1-3. URL: http://ijses.com/wp-content/uploads/2018/07/181-IJSES-V2N6.pdf
- Atashafrouz, Askar. „The effectiveness of chess on problem-solving, working memory, and concentration of male high school students.“ Iranian Evolutionary and Educational Psychology Journal4 (2019): 249-258. URL: https://doi.org/10.29252/ieepj.1.4.2
- GÜNDÜZ, Nevin, and Ü. N. E. R. Umut. „Application and Evaluation of Peer Education Model in Chess Learning.“ The Journal of Eurasia Sport Sciences and Medicine3: 103-115. URL: https://dergipark.org.tr/en/download/article-file/1117499
- Sandoval-Tipán, Luis, and Carlos Ramos-Galarza. „Efectos del ajedrez en el funcionamiento neuropsicológico infantil de la memoria de trabajo y la planificación.“ Revista Ecuatoriana de Neurología2 (2020): 46-51. URL: http://scielo.senescyt.gob.ec/scielo.php?script=sci_arttext&pid=S2631-25812020000200046
- TANAJYAN, Kristine, Nelli MELKONYAN, and Sirarpi MOVSISYAN. „Chess as a social value.“ Main Issues Of Pedagogy And Psychology1 (2021): 32-37. URL: https://miopap.aspu.am/index.php/miopap/article/download/390/352
- Gao, Qiyang, et al. „Does perceived chess skills mediate the relationship between fluid intelligence and academic performance?.“ Journal of Psychology in Africa1 (2021): 56-60. URL: https://www.researchgate.net/profile/Chen-Wei-3/publication/349917758_Does_perceived_chess_skills_mediate_the_relationship_between_fluid_intelligence_and_academic_performance/
- Glukhova, Oksana V. „The Need for Chess in School and Its Role in the Dynamics of Child Development.“ Revue internationale du CRIRES: innover dans la tradition de Vygotsky1 (2017): 161-168. URL: https://psyjournals.ru/journals/cpp/archive/2022_n4/Glukhova_et_al
- Chitiyo, George, et al. „Students’ perceived benefits of chess: Differences across age and gender.“ Journal of Global Education and Research3 (2023): 214-225. URL: https://digitalcommons.usf.edu/jger/vol7/iss3/2/
Downloads – Beitrag als PDF-Datei, Anhänge A-C als PDF-Dateien
Beitrag mit den Anhängen A bis C als PDF-Datei: Download
Anhang A „Übersicht wissenschaftlicher Arbeiten zu Schach in der Schule“ als PDF-Datei: Download
Anhang B „Verhältnisgleichung statt Dreisatz“ als PDF-Datei: Download
Anhang C „Zitate über Schach“ als PDF-Datei: Download
