MORE LEARNING SUCCESS – WHAT CHESS AND STEM-SUBJECTS CONNECT WITH EACH OTHER
(English translation of the German article “Plädoyer für Schach in der Schule” using the translation software www.deepl.com)
„The Game of Chess is not merely an idle amusement. Several very valuable qualities of the mind, useful in the course of human life, are to be acquired or strengthened by it, so as to become habits, ready on all occasions. For life is a kind of chess, in which we have often points to gain, and competitors or adversaries to contend with, and in which there is a vast variety of good and ill events, that are, in some degree, the effects of prudence or the want of it.“ (Benjamin Franklin)[1]
The strength of Germany as an industrial nation is based on scientific know-how and engineering skills. Attractive professions with good earning potential, which include STEM professions, require sufficiently good mathematical skills and good language skills. The shortage of skilled workers and the creation of future prospects dictate that everything possible must be done to make it easier for pupils to acquire mathematical knowledge and language skills and to pave the way for STEM professions. Unfortunately, various studies conducted in recent years attest to deteriorating knowledge and skills in mathematics among German students. The results of the survey conducted in 2018 with ninth graders on how they assess mathematics lessons give clear indications of effective measures to improve performance:
„Within the framework of the study, the theoretically proposed thesis that mathematics lessons systematically educate students to avoid mathematics could be empirically confirmed. Across schools, federal states and school types, current mathematics lessons produce large groups of students who are not interested in mathematics and who, moreover, have learned to associate the study of mathematics with discomfort. This supports the assumption that mathematics lessons contribute to educating a part of the students to become avoidant sufferer of mathematics…“[2]
The ancient and worldwide popular game of chess is still a useful tool in the 21st century to master the challenges of the age of computers and artificial intelligence. Worldwide research shows that playing chess leads to better school performance. In addition, chess is an cost-effective way to make it easier for pupils to learn about maths and science, because chess can be played anywhere and the necessary equipment is not expensive. In chess, students learn different skills through play, which have a positive impact on the science subjects and personal attitudes of the students. In this script “Why we should have chess at school”, the resources for more learning success that can be found in regular chess lessons are described. First, some preliminary considerations are discussed.
Table of contents
1. MATHEMATICS AND GERMAN LANGUAGE – SKILLS OF PUPILS IN GERMANY
1.1. CAUSES OF PROBLEMS IN MATHEMATICS AND GERMAN LANGUAGE
1.2. FEAR OF THE SUBJECT OF MATHEMATICS AND THE STEM-SUBJECTS
1.3. WHAT SKILLS ARE NEEDED IN MATHEMATICS AND THE STEM-SUBJECTS?
2. PATTERN RECOGNITION IN SCHOOL SUBJECTS SUCH AS MATHEMATICS, GEOMETRY, GERMAN LANGUAGE
2.1. MATHEMATICS IN SCHOOL – PATTERN RECOGNITION
2.2. PROBABILITY CALCULATION – PATTERN RECOGNITION AND MENTAL ANTICIPATION
2.3. GEOMETRY IN SCHOOL – PATTERN RECOGNITION AND PLANNING
2.4. LANGUAGE AND PATTERN RECOGNITION
3. PROBLEMS IN MEASUREMENT OF LEARNING SUCCESS
4. LONG-TERM PERFORMANCE SUCCESS IN LEARNING BY PLAYING CHESS
5. CHESS PROMOTES INCLUSION SUSTAINABLY
6. WHY CHESS HAS A POSITIVE EFFECT ON MATHEMATICS AND THE STEM-SUBJECTS
6.1. CHESS PLAYERS THINK IN IMAGES
6.2. CHESS ENCOURAGES CREATIVE PROBLEM SOLVING
7. WITH THE LEARNING-DIDACTIC GAME “CHESS” COST-EFFICIENTLY TO MORE LEARNING SUCCESS IN SCHOOL
REFERENCES
APPENDIX A OVERVIEW OF SCIENTIFIC PAPERS ON CHESS IN SCHOOLS
Downloads – Article as PDF file, Appendices A to C as PDF files
“Why we should have chess at school” in German

Wikinger Chess Set, brass and copper sheet metal, Artist: Andrzej Nowakowski
1.MATHEMATICS AND GERMAN Language – SKILLS OF PUPILS IN GERMANY
According to the IQB Education Trend 2021, the competencies of fourth graders in German and mathematics have deteriorated significantly. The proportion of pupils who fall short of the minimum standard in Orthography is about 30 percent for Germany as a whole. The proportion of fourth graders who meet or exceed the standard in orthography in Germany as a whole is about 44 percent, i.e. less than half.[3]
The percentage of fourth graders who achieved at least the regular standard in the competence area of reading fell to 58 percent in 2021.[4] This is more than alarming, since the competence “reading comprehension” is needed to solve the word problems in mathematics, chemistry, physics, biology and geography.
The proportion of high performers students who meet or exceed the standard has decreased in German and mathematics. At the same time, the proportion of students who do not reach the minimum standard and thus have a high risk of a less successful educational careers has increased in all areas of competence, in part significantly.[5]
How does it look in higher grades? According to the latest PISA study from 2018, the mean mathematic competence of fifteen-year-olds in Germany decreased compared to PISA 2015 and PISA 2012. Compared to the peak achieved in PISA 2012, PISA 2018 shows a significant decline in mathematical competence. Furthermore, it is found that since PISA 2003, the mean scores of mathematical literacy at high schools have been decreasing almost continuously. In PISA 2015, students at grammar schools already achieved weaker results than in the surveys of previous PISA studies.[6]
In particular, the proportion of pupils at non-grammar schools who only reach the lowest levels of competence is very high at just under 30 percent. These have a particularly high risk of dropping out of school without a lower secondary school certificate.
While the mathematical competence of girls in Germany has remained largely unchanged compared to PISA 2012 according to the 2018 PISA study, it has significantly decreased by almost 17 points among boys since 2012.[7]
The rate of young people with an university or technical college entrance qualification has fallen since 2014. In contrast, the number of school leavers who have not attained at least a lower secondary school leaving certificate has increased in the same period. (Spiegel, 23.06.2020)[8]
In 2019, a remarkable letter was written to the Standing Conference of Ministers of Education and Cultural Affairs, signed by hundreds of professors, scientists and personalities. The letter complained that hardly anything has changed positively in the “mathematics” curriculum since the urgent letter from hundreds of professors in 2017.[9] The actuality of the above-mentioned urgent letter can be illustrated by the example of percentage calculation. There are mathematics educators who see little opportunity for mental arithmetic strategies in the solution scheme of the rule of three (see Fig. 1).
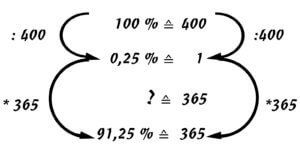
Fig.1 calculation scheme of the rule of three
From a longitudinal study on percentage calculation in mathematics lessons, it is known that learners of all school types solve a relatively large number of tasks, but achieve less than 50 % correct solutions nationwide.[10] In many schools, the solution scheme “rule of three” is taught to solve percentage problems. The assignment to the terms basic value, proportionality factor causes difficulties. A change from the solution scheme “rule of three” to the solution scheme “ratio equation” does not seem to be possible for the time being. The solution pattern “ratio equation as fraction equation” is not very popular among didacticians.[11] In the opinion of the author of this article, the rule of three has many disadvantages in terms of learning comprehension and application in other subjects. (see Appendix B)
Today we live in an information society that constantly demands people to learn new knowledge and technologies. Those who have the necessary personality qualities and skills, such as willingness to learn, motivation, sense of responsibility, reliability, flexibility, conscientiousness, self-confidence, openness, attentiveness and the ability to concentrate, are better able to cope. The economy is in global competition for well-qualified skilled workers. The availability of qualified skilled workers also plays a role in decisions about investments in new locations or expansions of existing locations.

1.1. CAUSES OF PROBLEMS IN MATHEMATICS AND GERMAN LANGUAGE
The use of newspapers and magazines has changed greatly in recent decades. In the 19th and 20th centuries, newspapers and magazines offered all kinds of challenging puzzles for entertainment. Tour puzzles in small and large fields, chess and checkers puzzles, detective riddles, language games.

Fig.2 Puzzles from the magazine „Gartenlaube“, 1890[12]
Such challenging brain twisting puzzles are rarely found in today’s magazines and newspapers. On the internet, you have to consciously search for such offers and go to websites or find and download suitable apps in the app store. The casual engagement with such puzzles and the casual learning through solving such puzzles is more difficult today.
„When children are at war with mathematics, experts often diagnose them with so-called dyscalculia. But this term unfairly places the blame on the affected children themselves, says mathematics didactician Wolfram Meyerhöfer from the University of Paderborn. Every child can learn arithmetic – with the right methods.“[13]
Pupils with particular difficulties in learning mathematics in primary school have difficulties in moving away from counting arithmetic to thinking arithmetic. Counting arithmetic takes more resources in the brain, takes longer and has its limits when calculating with larger numbers. It is becoming increasingly difficult to make learning progress. Prevention is exercises in breaking down, comparing, quantifying quantities. Successful prevention relies on the ability to identify and name structures and quantities that the learner must have or acquire. Many students have problems with multi-digit numbers in that they perceive the multi-digit numbers as a sequence of digits rather than recognising the pattern of numbers[14], for example, that two-digit numbers are made up of tens and ones or the three-digit numbers are made up of hundreds, tens and ones.
Arithmetic fails – “if the number breakdowns up to and including ten have not been fully automatised and already automatised problems cannot be used for derivations [pattern matching], the pupils are left with counting as the only available solution tool, in addition to the recall of already automatised arithmetic problems. Automatisation on their part, however, is at least made more difficult by the permanent practice of counting arithmetic.”[15] For its part, the required automatisation presupposes that the necessary information is available in patterns and images, which are interrelated, in a library in long-term memory, ready for retrieval. The main advantage of automatisation is that automatic processes can run in parallel, are resource-efficient, and do not require significant attention and concentration. Working memory is the bottleneck to long-term memory. The incoming information in the brain is processed in the working memory, i.e. the information is identified, compared, evaluated, coded and stored. The development of the working memory determines its performance. An insufficiently developed working memory hinders the reception and processing of information, which has a negative effect on learning performance.
“If, for example, mathematics lessons are concerned with the development of mental images, such as that of the 20-field, it must be assumed that children with better working memory resources have an advantage in the development of knowledge. Thus, compensation for deficient working memory functions appears necessary to create better learning conditions.” The addition of multi-digit numbers is accompanied by complex information processing in the working memory: In multi-digit mental addition tasks, the working memory not only stores the addends and retrieves the result from the long-term memory, but also holds intermediate results and initiates and monitors the selection and execution of complex calculation algorithms.[16]
In particular, grammatical skills influence mathematical learning in the long term.[17] Grammar contains the rules of language and describes the structure of language. The sentence structure has an influence on what additional information is perceived. For example, the order of individual words can increase or decrease the information value of individual objects described by them. Even more difficult is the communicating of phonetic information, because the particular emphasis of a word can lead to different perceptions of the information, for example, that action is being called for or that an accusation is being made. It can be concluded from this that a minimum of technical language vocabulary must be available in order to receive and process the information obtained through language according to its actual intention, i.e. to recognise, compare, assign and evaluate it. The more language vocabulary there is, the better communication is possible because facts are better captured, understood and reflected upon, which is of great importance in relation to the STEM subjects.
The subject of physics is considered particularly difficult by pupils. Physical processes are described in the language of mathematics. The linguistic description of the physical process cannot represent the underlying mechanisms and knowledge in the complexity and diversity that the corresponding physical formulae in mathematical notation can. The mathematical equations found are themselves part of the process of knowledge. In atomic physics there are many examples of predictions of particles whose existence was only confirmed much later by extremely complex experiments. The reduction of real processes to mathematical symbols and equations causes difficulties for learners For understanding and learning success in physics as well as in other natural sciences and in many areas of economics, it is important to be able to interpret the mathematical equation, i.e. to derive further knowledge from the equation.
Example: Speed
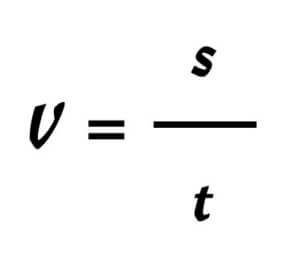
Fig.3 v – speed, s – distance, t – time
The speed is the distance moved within a given time. The equation contains much more information than the fact just mentioned. The inherent dynamics become visible with the interpretation. The greater the distance moved in the same unit of time, the greater the speed, or the less distance moved in the same unit of time, the smaller the speed. However, one can also read out that at the same speed, the distance moved increases as the duration of time increases. In everyday language, one would say: “The longer one drives, the more distance is travelled. After converting the formula, this relationship can be read off directly:
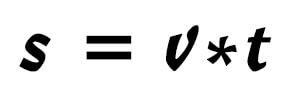
Fig.4
Everyday experience is contained in the equation. The interpretation of the results requires practice, because the mathematical results have to be translated into the real world. The term “power” occurs in physics as well as in economic science and is defined the same as “power equals work per unit of time” .[18]
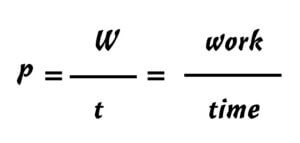
Fig.5 Power
The difference lies in the interpretation of the term “work”. In physics, work is a quantity of energy, whereas in economics it is the (quantitative) output.
The trend of easy language found in many cases in Germany needs to be seriously reconsidered. Vocabulary exercises such as semantic fields make it clear that language is a powerful tool for describing reality. Good expressiveness builds on a rich vocabulary. Accurate word choice improves expressiveness and reduces misunderstandings in communication. The technical language reflects the world of thought of the respective subject and standardises the terms of everyday language to the respective subject area. Another key factor for the child’s mental and psychomotor development is the expansion of vocabulary, because children need new information to develop a thought filter that enables choice.[19] There seems to be a misconception that “easy language” is really easier to understand:
„With their statements in the reflection interview, the pupils […] only partially confirmed the assumption that technical terms complicate a physical problem. In fact, a problem with technical terms and new concepts only seems difficult to them at first glance. On closer inspection, however, the technical terms prove to be helpful in finding formulas, because without the technical terms, things that are familiar from the lessons and essential for the work are missing.“[20]
1.2. FEAR OF THE SUBJECT OF MATHEMATICS AND THE STEM-SUBJECTS
„To those who do not know mathematics it is difficult to get across a real feeling as to the beauty, the deepest beauty, of nature. … If you want to learn about nature, to appreciate nature, it is necessary to understand the language that she speaks in.“ (Richard Feynman)[21]
We know from sport and medicine that self-confidence and willingness are powerful factors for success. Fear, on the contrary, encourages failure. It is therefore not surprising that the expectations of success that one ascribes to oneself in the respective occupational field play a major role in finding a profession. Confidence in one’s own abilities also influences how much energy is spent on learning new skills. The attitude that one is basically good in a certain discipline – such as mathematics – also leads to a greater willingness to invest more time in working on new problems, because one assumes ex-ante that one will succeed in solving the problem. (Lin-Siegler et al., 2016).
Personal attitudes and beliefs have a major impact on learning success, Students’ belief and conviction that success in science depends on special talents has a negative impact on their motivation to learn. It has been shown that such beliefs are reasons why students dislike science and mathematics subjects. [22]
Telling students that even successful scientists experienced failures before their discoveries can help them to understand their difficulties in science classes as normal events and not as an expression of a lack of intelligence or talent for these subjects. A promising way to get students more interested in science was to show them the difficulties scientists had to overcome on their way to making discoveries.[23] In this way, students learn that diligence and perseverance pay off in the end. Counter-productive are the many statements by celebrities in the media who surpass each other in explaining how difficult mathematics is. There must be a societal change:
„It is also about improving the image of maths in society in order to get more young people interested in the subject. However, according to Professor Weitz, there is often still a cultural, social phenomenon in which it is implicitly made clear to everyone from the outset that maths is frustrating This way of thinking inhibits learning.“
(Edmund Weitz, Professor of Mathematics and Computer Science at the Hamburg University of Applied Sciences/ HAW Hamburg)[24]
We know from experience that fear has a paralysing effect. Fear of mathematics is a serious obstacle on the way to better mathematical skills.
„Mathematics anxiety is a performance-related emotion that describes a feeling of tension, apprehension or fear when dealing with mathematical problems in daily life and at school. Mathematics anxiety is negatively related to subject matter competence and mathematical self-concept and contributes to the avoidance of situations that involve mathematical demands. (e.g. choice of course of study or job with mathematical content; Pekrun, 2006).“[25]
The study “IQB-Bildungstrends 2021” also registered pupils’ anxiety. Almost every fourth child (23%) reported high anxiety for the subject mathematics. Less than half of the children (40%) reported low anxiety in mathematics. Maths anxiety often means avoiding more mathematically demanding occupations, many of which offer better earning opportunities than “non-mathematical” occupations.
The number of pupils who are afraid of mathematics has increased in Germany in the past. Against the background of the shortage of skilled workers, everything should be done to reverse this trend as quickly as possible.
How can mathematics teaching be made more promising? Successful teaching-learning processes are hardly related to a specific methodical lesson design or view structure, but the deep structures are decisive, which relate to the quality of the learners’ engagement with the learning content and the students’ interactions with each other and with the teacher.”[26]
Deep structures are the psychological-pedagogical process qualities of teaching, such as cognitive activation, adaptive learning support or clarity of understanding. Deep structures can be assessed with three teaching quality dimensions:
- Classroom management. It is about ensuring that the students can use the learning time effectively, for example, by preventing disruptions an arranging for clearly structured processes in the classroom.
- Constructive learning support. This includes aspects such as feedback, learning process support, error culture – i.e. the question of whether errors are also seen as learning opportunities.
- Cognitive activation. The focus here is on whether good problems are set that differentiate, are stimulating and can be solved at different levels of competence.[27]
There are no simple solutions. One possible way can be the playful moment in the classroom, where many important competences are promoted at the same time. „Chess is such a game involving activities that can provide children with joyful playing experiences and arouse their interest to explore the symbols, cultures and rules involved at the same time. It is a game with farreaching universal popularity and easily recognizable concept and basic rules that are sufficiently simple to be taught to children.“[28]
Chess has proven its qualities in improving students’ mathematical performance in many international studies. What are the reasons that chess brings about visible improvements in academic performance, especially mathematics?
1.3. WHAT SKILLS ARE NEEDED IN MATHEMATICS AND THE STEM-SUBJECTS?
„What humans do with the language of mathematics is describe patterns“ (Lynn Arthur Steen, 1990)[29]
To answer this question, the thinking and approach of scientists is considered. „Scientific thinking, defined as intentional knowledge seeking, encompasses the abilities to generate, test, and evaluate hypotheses, theories, and data, and to reflect on this process.“[30]
Mathematics is understood as the science of patterns. „Patterns are often expressed through relationships and functions. Tables, charts, formulas, and graphs are among the many devices used to represent patterns and relationships (e.g., between Centigrade and Fahrenheit, miles and kilometers, speed and time, principle and interest). Relationships establish connections and document dependencies; they reveal correlations or confirm independence. Some relationships are direct, others inverse; some show steady trends, others oscillate; some are smooth, others discontinuous. Most can be represented in multiple forms–graphically, verbally, numerically, or analytically. Indeed, the patterns of mathematics are often revealed most effectively through the interplay of these multiple representations.“[31] In summary, solving mathematical problems is based on the knowledge and application of various techniques and methods of pattern recognition.[32]
In chemistry and physics, thinking models are used that reduce reality to its essential content and idealise it. Facts and processes are represented with mathematical symbols and equations. In the course of gaining knowledge, the thinking models are expanded and adapted. Mathematical methods are necessary to understand relationships, to describe natural processes, to find solutions and to evaluate results.
Word problems in science subjects usually reflect real possible events. The aim of text problems is to achieve practical relevance and to enable students to apply mathematical and scientific methods. The way to the solution is to find an adequate mathematical or scientific pattern that comes closest to the problem.[33] This requires the ability of
- of comprehending reading to understand the content
- to analyse in order to determine the complexity of the tasks and to derive individual subtasks,
- to plan and structure in order to determine the approach and sequence,
- to evaluate in order to validate the solution found des Bewertens, whether the result obtained meets the requirements of the problem
In the USA, research results have been published on the problems students have in physics lessons.[34] Understanding the problem and the physical context are preconditions for successfully mastering the problems. Knowledge application builds on the existence of effective heuristics for problem solving. The capacity of the working memory and the way in which the knowledge (information) is stored in the student’s long-term memory determine how effectively the problem can be solved. Measures such as analogical thinking, group work, stronger self-reflection, thinking through the task with external instructions are seen as a proven way of helping students to learn successfully.
Training pattern recognition and working memory must be the key to more learning success at school. Homework is given at school so that the student can reflect on, explore and internalise the knowledge taught in lessons. Writing and conducting experiments support the process of acquirement of knowledge and internalisation. Science confirms the experiences described here:
Most researchers are in agreement that pattern recognition based on pre-stored knowledge is one of the main reasons for the superior performance of experts.[35]
But how can children train the ability to recognise patterns? Chess is a game that trains the ability to filter information and to recognise patterns. The game of chess can provide excellent services as a didactic learning tool.
2. PATTERN RECOGNITION IN SCHOOL SUBJECTS SUCH AS MATHEMATICS, GEOMETRY, GERMAN LANGUAGE
„Man is still the most extraordinary computer of all.“ (John F. Kennedy)[36]
2.1. MATHEMATICS IN SCHOOL – PATTERN RECOGNITION
Like words are made up of letters, numbers are made up of digits. Foreigners who learn the German language have trouble at first with how Germans say numbers in words:
| Number | German | English | French |
| 21 | Einundzwanzig | twenty-one | vingt et un |
| 22 | zweiundzwanzig | twenty-two | vingt-deux |
| 233 | zweihundertzweiundzwanzig | two hundred and twenty-two | deux cent vingt-deux |
The German first says the one and then the ten. This leads to irritation. This can be a problem for children with a migration background, which must be eliminated through practice and active speaking.
Every language has its own peculiarities. The numbers 70, 80, 90 and 95 in French are similar to an arithmetic problem:
| 70 | soixante-dix | 60 + 10 |
| 80 | quatre-vingts | 4*20 |
| 90 | quatre-vingt-dix | 4*20 +10 |
| 95 | quatre-vingt-quinze | 4*20 + 15 |
It cannot be deduced from this that the German language is easier or harder than the French language or that the children of one country learn arithmetic more easily.
Solving mathematics problems, especially in the lower grades, is, to say it simply, about pattern recognition. There are many advisors and didactic aids that explain how children learn to add numbers beyond the number range greater than 10. Ultimately, this task is based on pattern recognition. Because addition according to the following pattern:
10 + 1 =11
10 + 8 =18
20 + 7 = 27
60 + 9 =69
makes it clear that with this type you simply replace the ones digit “0” with the one-digit summand to obtain the solution. That is, you replace the image of “0” with the image of the one-digit summand. This pattern can then be transferred to more complicated addition tasks. Other patterns come into play in mental arithmetic.
The multiplication table must have been internalised. An old-style primary school teacher once explained it to primary school pupils like this: “If I wake you up at night and give you a task, the answer must come so fast that they seem to have been shot from a gun.”. These simple basic tasks are used to solve more complex arithmetic operations. Therefore, it is important that children write the entire maths problem on their paper and only then complete the solution. In this way, they memorise the task as a pattern image.[37]
2.2. PROBABILITY CALCULATION – PATTERN RECOGNITION AND MENTAL ANTICIPATION
The introduction to probability calculation often starts with examples of coin tossing, throwing dice or different coloured balls in a box.
In the practical test, the children experience: The more coin tosses happen, the more the total numbers of the events “number” and “coat of arms” approach each other – the ratio 50:50 with regard to the total number of tosses. The visualisation can be done by keeping a tally sheet for the respective events “Number” and “Coat of Arms“.
The question of the probability of drawing a blue ball when there are 3 blue balls, 2 red balls and 5 green balls in the box requires a planned approach to find the correct solution. Experience helps to a limited extent, because in a self-experiment you can hold a blue ball in your hand immediately with the first grip or only with the sixth grip in the box. Now, similar to the coin toss, you can approach the actual result through many attempts, but this is very time-consuming. It is more important to think economically by not considering the ideal case of having the blue ball on the first pick, which would then correspond to a probability of one. In your mind you play through the unfavourable scenarios. It helps to imagine the box with the coloured balls and to visualise which balls remain in the box when you take a ball out. You will notice that in order to solve the task, you have to find the worst case. In the present case, the worst case is that all red and green balls are drawn first before a blue ball is picked with certainty. Now the mental result must be represented in the language of mathematics.
In the course of mathematics education at school, new patterns are added and combined with previous ones. Scientists use different “calculation tricks” to simplify and solve equations and fractions. The aim is to reduce complicated terms to simpler terms for which solution methods are known. Typical methods are substitution procedures, use of the binomial formulae. Recognising and applying calculation advantages means: having self-confidence in one’s own abilities as well as expanding and optimising an existing spectrum of solution patterns.
2.3. GEOMETRY IN SCHOOL – PATTERN RECOGNITION AND PLANNING
Geometry is pure pattern recognition. Geometric shapes are used to explain the concepts of set theory. Objects with similar properties are grouped together to form sets.
| Total quantity | Quadrilaterals | Trapezoid | Rectangle |
| Partial quantities | Parallelogram | Parallelogram | Square |
| Rhombus | Rectangle | ||
| Rectangle | Square | ||
| Square | |||
| Trapezoid |
In plane geometry, a rectangle is a quadrilateral whose interior angles are all right angles. This also means that the opposite sides are parallel to each other. The rectangle is a special case of the parallelogram and thus also of the trapezoid. With the parallelogram, the opposite sides are parallel. The diagonally opposite interior angles are equal. With a trapezoid, 2 sides are parallel to each other. A special case of the rectangle is the square, where all sides are also the same length. These different terms are part of the technical language “geometry”, which does not exclude that some of these technical terms are often encountered in everyday language.
When drawing geometric figures to scale, the procedure must be planned in the mind and the sequence of steps analysed. Depending on the information available, there are different procedures for drawing the geometric shapes.
EXAMPLE TRIANGLE
If one side (AB) and two angles (1,2) of triangle ABC are given, then proceed according to the following scheme:
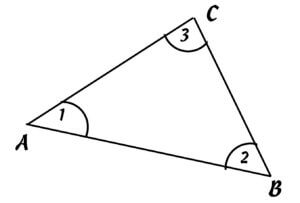
- draw a line AB (known side)
- draw a straight line through the intersection point A with angle 1
- draw a straight line through the intersection point B with angle 2
- the point C of the triangle is the intersection of the lines from 2 and 3
If all sides of the triangle (AB, AC, BC) are known but not the angles:
- draw line AB (known side)
- draw an arc with radius=AC from point A with a compass
- use the compass to draw an arc with radius=AB from point B
- the point of intersection of the two arcs from 2. and 3. is connected with points A and B.
Pattern recognition is useful in planning by visualising the known sizes of the triangle. Pattern recognition, visualisation and mental planning of the process steps also lead to success in other school subjects.
2.4. LANGUAGE AND PATTERN RECOGNITION
Language and reading are also finally about pattern recognition. The single letter usually has no meaning. Only the sequence of several letters results in a word, which is stored both as a visual image in the form of the word and as an overall combination of single letters. The sequence of single sounds that correspond to letters or groups of letters (“sch”, “sp” – German Language) in the visual language results in the pronounced word. The sequence results in a sound image, which is stored in connection with the object, the event or the action. The sound image of the words contains additional information compared to the written language and can trigger feelings. From the sound image it can be inferred whether it is a question, statement or request, whether the speaker is in a hurry, whether the speaker is bored or interested, … Deaf people have great difficulty in pronouncing words in such a way that they can be understood effortlessly by their non-deaf counterparts. Deaf people lack their own means of control, namely to compare the sound of the word.
In contrast to mathematics, it is possible to communicate and exchange information in everyday life without knowledge of letters and spelling. A foreign language can be learned without knowledge of the written word and the letters, as can be observed, for example, in children growing up bilingually. It is irrelevant whether it is a language that is visually represented with Latin letters or Cyrillic letters. Different areas of the brain are activated for hearing and seeing.
Grammar is the set of rules of the language. It describes, among other things, how the tenses are formed. Here, too, it is a matter of pattern recognition. In different languages, a distinction is made between regular and irregular verbs. Regular verbs have fixed patterns of conjugation in the tenses. Theory of word formation provides patterns and methods for word formation. Thus, various typical endings give indications as to what type of word it is, for example, whether it is a noun or an adjective:
German language
| Typical endings for adjectives | Typical endings for nouns |
| -lich | -ung |
| -sam | -heit |
| -ig | -keit |
| -isch | -schaft |
| -bar | -tät |
| -haft | -tum |
| -arm | -nis |
3. PROBLEMS IN MEASUREMENT OF LEARNING SUCCESS
As indicated above, the knowledge acquisition and the enhancement of school performance is a very complicated process with many influencing factors. Despite the most modern scientific methods and techniques, there will never be 100% certainty in all details.
The main problem of research in the field of education in general is that the study participants cannot simply be isolated for a certain period of time. Rather, they are in permanent exchange with their environment, are subject to moods and mood swings, have a changing sense of well-being and changing energetic states every day.
Not all teachers are equally good at getting pupils excited and involved in the subject or game of chess. There are pupils who have an aversion to teaching and as a result show little motivation to learn and make less effort to achieve good results in the subject. Children are still in the growth phase, i.e. as they get older, changes in perception, vision and behaviour occur. Each person naturally brings different prerequisites with them in the form of their genes. Researchers are faced with immense challenges in developing suitable experimental designs to test the effectiveness of measures to increase learning success.
The requirements in the training occupations and fields of study are characterised by change. Knowledge transfer must adapt to the changing conditions. Imparting knowledge has always been a challenge. Everywhere, skilled workers are being sought who are also expected to have different personality traits. Education in particular shows that a lot of money does not automatically help a lot.
Decision-makers in politics, business and administration like concrete facts and results to prove that the desired goals will be achieved. When the idea of “chess in schools” to improve academic performance is put forward, it is very often followed by a demand for evidence on the effectiveness of chess to improve learning. There are hundreds of studies that prove the learning success of chess and each study has strengths and weaknesses in terms of experimental design.
What is the situation regarding current topics at school? What scientific evidence is there on the effectiveness of various teaching measures, for example interdisciplinary teaching? What findings are there for the effectiveness of extending the lesson from 45 minutes to 60 or 90 minutes with regard to the desirable goals of more knowledge gain and more learning success, especially against the background that educators repeatedly complain about the lack of concentration and attention among pupils? A study published in 2021 states: Empirical insights into whether the expectations associated with the changed lesson time have been confirmed are hardly available for the German school system so far.[38] Subsequently, the results of three examined grammar schools (125 teachers and 803 students) were presented. The aforementioned paper did not present whether the lengthening of the lessons led to better levels of knowledge and better grades among the pupils, how the lengthening of the lesson affects the concentration and attention of the pupils. What is the effect of the longer lesson time at primary schools, middle schools, secondary schools and high schools, where more low-performing pupils learn than at grammar schools?
Interdisciplinary teaching has been propagated and implemented in schools for many years. The aim of interdisciplinary teaching is the transfer of knowledge and the linking of existing knowledge. Now, in 2022, Haunhorst et al sum up: “Student teachers acquire a wide range of competences in teaching their own subjects, but few competences in interdisciplinary teaching.“[39] Furthermore, it is pointed out that the data situation is insufficient and that there are major problems in the conception of a research design for the evaluation of interdisciplinary teaching. The necessity to consider the subject matter from different perspectives and approaches is seen as a condition for success. Further necessary conditions are the professional competence of the teachers and the ability of the teachers to cooperate with each other in the sense of interdisciplinary teaching. A total of 14 studies on interdisciplinary teaching with the combination of “sport and science subject” were identified in the Education Portal for the years from 2000 to 2019.[40]
Not so in chess. There are hundreds of studies investigating the impact of chess instruction on learner success in school. Despite the problems of conducting scientific research on the impact of chess on student achievement, there is a broad consensus that chess teaching has a positive impact on cognitive skills and performance in school subjects.[41]
For the published study on the “Chess Instruction Improves Cognitive Abilities and Academic Performance” in 2022[42], high demands were formulated for the research studies to be analysed. Three main criteria were formulated for the investigation design. 230 relevant scientific papers were identified in the databases, of which 45 papers satisfied the three main criteria.
There is no doubt that chess has positive effects on school performance. Criticism of the chess research is that it has focused too much on measuring the success of far transfer, that sample sizes have been rather small and that short-term rather than long-term effects have been investigated.[43] The research in the education and school sector, which is unrelated to chess, is also criticised because it tends to examine short-term effects.Watts et al.[44] They believe that the lack of studies with long-term follow-ups poses difficulties for developing educational programmes that perform well. The researchers complain that currently, correlations between short-term outcomes and long-term effects are often assumed but rarely tested with experimental methods.
Blanch examined the results of 45 selected papers from 19 countries (Argentina, Australia, Bangladesh, Belgium, Canada, Denmark, Germany, India, Iran, Italy, Malaysia, Romania, South Africa, South Korea, Spain, Turkey, the UK, Uruguay and the USA).[45] The two countries Russia and Brazil, which are among the most active countries in school chess worldwide, were not included. At the 2018 International Congress on Human Mental Health in the 21st Century, which was participated in by scientists from Germany, the USA, Great Britain, Chile, Portugal, Malaysia, India and other countries, the results of a long-term study on the effect of chess instruction on the intellectual development of children over their school career were published.[46] The research investigated the near-transfer effects. The results are impressive and are presented in the next section.
4. LONG-TERM PERFORMANCE SUCCESS IN LEARNING BY PLAYING CHESS
„One step in learning may mean one hundred steps in development.“ (Lev Vygotsky)[47]
In Russia, the subject “chess” is seen as an opportunity to give pupils the best possible opportunities for their development and academic success. Since 2004, a long-term study on the effects of chess lessons on personal and academic development has been running with various schools in the city of Satka (Chelyabinsk Oblast). Over 18 years, 1571 pupils were examined in the study, with 723 pupils being taught according to the “chess project” teaching programme, which was developed on the basis of the ideas of the psychologist Lev Vygotsky, the principles of the reflexive activity approach[48] and the Russian educational goal of “abiltiy to act in the mind”.[49] “Abiltiy to act in the mind” means going through different possibilities and processes in one’s mind and examine what happens when a step is taken, what further step might follow as a consequence and what its effect might be. Designing chess lessons based on the principles of the reflexive activity approach should enable students to consciously transfer the skills developed in chess lessons to other school subjects and activities. This transfer has an effect on the general development of the pupil, has a preventive effect against school failure and is reflected in better academic performance.
With scientific support, chess teaching manuals, workbooks and a chess programme for the school project were developed. The English version of the teaching materials and the first results of the study were presented to a broad public in 2017 in Quebec (Canada) at the international congress “Contemporary Russian Contributions to Vygotsky’s Heritage”, hosted by the International Society for Cultural-Historical Activity Research (ISCAR).[50] In the following years, further results of the chess research were made available to the public.
Detailed information on the first phases of the elaborate school chess study with many additional theoretical explanations was published in 2022.[51] In the first two phases, 637 pupils were studied, of whom 331 participated in the aforementioned chess programme.
Results of the first phase 2004 – 2008 (primary school period)
The pupils who were educated in chess according to the “Chess for General Development” (chess-project) programme made greater progress than the children in the control groups. They showed greater aural learning skills, improved visual memory, were better able to handle non-verbal reasoning tasks, became more attentive and efficient, and were better able to mentally plan their actions, as shown by the internal action plan discovery tests used. The results for three of these indicators increased steadily over the course of the year, which was evident in every examination: auditory memory, verbal intelligence and the internal plan of action. No negative dynamics were found for any of the indicators. None of the comparison groups showed such a significant trend for any of the indicators.
Results of the second phase 2010 – 2013
Two tasks were pursued here:
-
-
- observation of the development dynamics of children in a mixed class, in which there were four children with developmental disabilities. All of them are taught together according to the teaching programme “Chess for General Development” (chess-project).
- to test whether the high level of development of cognitive functions is maintained in children who took part in chess lessons with the “chess project” programme in primary school, compared to the groups who took part in the “chess universal” programme and who did not receive any chess lessons at all. The ninth graders studied have participated in the chess project and in psychological examinations since 2004.
-
Results for the two tasks
-
-
- from the results of the survey, it can be concluded that the second graders in the main group show positive developmental dynamics in 5 indicators: Memory (auditory and visual), non-verbal intelligence, working ability and the ability to plan actions in the mind. There is a statistically significant difference in these indicators between the May 2011 survey and the 2012 survey. The results for children with developmental disabilities varied, with some indicators showing higher scores.
- the comparison of the results of the main chess project group and the chess universal group showed that the main group had a higher level of development of non-verbal intelligence and higher attention scores.
-
Over the indicated period, a large number of pupils, both chess pupils and non-chess pupils, have generally improved their level of cognitive development. However, compared to the control groups, where chess was taught using other methods or not at all, the main group students have steadily improved their scores on a large number of intellectual indicators over the years.
According to the data, chess-playing pupils with different levels of intellectual development show a positive dynamic in the development of intellectual skills. A comparative analysis of the indicators revealed a high level of efficacy of chess teaching based on the reflexive-activating approach used.
As the results of the third phase (see below) showed, the positive development of intellectual skills in primary and secondary education had a positive effect on learning performance in various subjects.
Results of the third phase 2014 – 2021
The positive impact of the chess lessons was even greater than expected. The students became more self-confident, learned to plan their tasks independently, were able to reflect on their successes and failures, their attitude towards mistakes changed and their personal potential in terms of self-efficacy was increased. As a result, the students achieved good academic results. The number of school leavers who received medals for special learning achievements increased.
In view of the positive results in the third phase, other factors were included in the investigation to learn more about learning motivations, coping with difficult situations independently, school anxiety, etc. Since 2017, research has also been pursued in this direction. Work on the analysis of all diagnostic results continues and will be presented in further publications.
5. CHESS PROMOTES INCLUSION SUSTAINABLY
The special qualities of chess also make the game interesting for the purpose of therapy. For some years now, there has been a worldwide trend to use chess in therapy, to develop new forms of therapy and to achieve healing successes. The focus of treatment with chess is on children suffering from bipolar disorders, depression, ADHD and behavioural disorders.[52]
The number of children diagnosed with ADHD is increasing every year. Scientific studies see a connection between extensive use of the smartphone/internet and the diagnosis of ADHD.[53] Attention deficit disorders such as ADHD have a negative impact on school performance. Medications prescribed for ADHD are a financial burden on social systems and have unwelcome side effects. If extensive smartphone use is the cause of ADHD, then there should be a hope of at least significantly alleviating the ADHD impairments because attention can be trained. Regular chess training to improve attention reduces ADHD problems, according to a large research review.[54] In 2021, the first clinical study was published showing that regular chess training as a therapy significantly improved the cognitive performance of ADHD patients. Patients reported that their general mood and interpersonal relationships improved.[55]
German researchers were one of the first in the world to present a study in 2008[56] that investigated the effects of teaching chess in classes of children with learning difficulties. German researchers were one of the first in the world to present a study in 2008 that investigated the effects of teaching chess in classes of children with learning difficulties. The aim of this comparative approach was to find out whether the special teaching method of chess in mathematics lessons leads to better learning successes for children with learning difficulties. The chess game is supposed to help the pupils to improve their attention and subsequently lead to higher basic mathematical skills in the children with learning disabilities. The experimental group exchanged one mathematics lesson for one chess lesson. At the end of the school year, the improvements in the children’s numeracy and concentration skills were compared between the experimental group, which received chess lessons instead of one hour of regular maths lessons per week, and a control group, which received only regular maths lessons. The experimental group had a clear advantage in improving basic mathematical skills such as counting and addition. Chess as an element of mathematics education in schools for children with learning difficulties can be a valuable learning tool.
The topic of inclusion has also reached Germany. The aim is to enable people with disabilities to become empowered to be equally integrated into society. Preparing children with intellectual disabilities for a self-determined life is an extremely difficult task. How can we pave the way for them to find a job that will enable them to earn their own living? Here, too, there are impressive results of how chess can completely change seemingly fixed predetermined way of life and make dreams come true:
In 2022, a German disabled player made fantastic headlines:
„And then Jarno Scheffner becomes world champion.
He is considered “mentally handicapped”. But when he starts playing chess at the age of eleven, it changes his whole life”. (11.08.2022, Zeit online)[57]
Jarno Scheffner: He has an IQ of 59 and goes to a special school for the mentally handicapped. A teacher taught him how to play chess and he loves the game. Today he works as a gardener.
And the other good message is that apparently children with developmental disorders can be helped with systematic chess training. The chess project in the Russian town of Satka (Chelyabinsk Oblast) gives hope (see previous section).
Sidorenko’s chess study, also published in 2022[58], is another example of the power of chess as a learning tool in combination with the reflexive activity approach. In 10 months of chess lessons and with other rehabilitation measures, a 30-year-old man has come an amazing way. At the beginning, the man led the life of an ordinary resident of a psychoneurological boarding school and was classified as legally incompetent He was taking medication, with no perspective of improving his condition, was without future perspective. After 10 months of chess training, he is already a new person: he lives with his family instead of in a boarding school, gets along without medication, works, makes professional plans and wants to marry. The main goal – the rehabilitation of his legal capacity – has been achieved. This individual case shows that the chess teaching programme developed in Satka, with the support of psychologists, can also enable disabled people to lead a self-determined life.
6. WHY CHESS HAS A POSITIVE EFFECT ON MATHEMATICS AND THE STEM-SUBJECTS
The increasingly worse learning results of German pupils demand that countermeasures be taken. The question is whether it is necessary to invent new concepts or to fall back on existing concepts that are scientifically supported.
From a philosophical perspective, chess can be regarded as mathematics: “Chess is mathematics because it is purely relational: chess pieces have no functions other than those they fulfil in the game (their shape is only a reminder of what piece it is). Chess is not normally considered serious mathematics because the rules are arbitrarily chosen (and because the question of what constitutes good strategy in human chess depends on an external, contingent fact, namely the intelligence of the players). But the existence of a knight tour over the complete chessboard, the solvability of chess problems published in newspapers with a certain configuration and the instruction “Black mates in two moves” and the abilities of AlphaZero[59], to play chess on a superhuman level are all pure mathematics.“[60]
So far as the theory goes. But what happens in the human brain during a game of chess? The more you examine the processes that take place during a game of chess, the more factors you recognise that are also beneficial for learning success at school. Training pattern recognition and the influence of regular chess training on personality development seem to be the strongest factors. They are also the factors that are most difficult to measure. Some processes that take place during a game of chess are examined in more detail.
Brain research found that the human brain processes images 60,000 times faster than text. 90 percent of all information transmitted to our brain is visual. As stated above, mathematics can be understood as the science of patterns. To be successful in pattern recognition, the brain needs a huge library of images and patterns, with additional information such as experience, usefulness and links to other library content.
Chess offers good conditions for training the brain in pattern recognition in a playful way. The game of chess is very complex. An enormous amount of information has to be processed for each move. When calculating several moves in advance, different movement patterns of the chess pieces have to be processed. Chess players develop skills to cope with the flood of information, to use the brain’s resources economically. The focus is on the efficient selection of chess moves that are worth analysing in more detail. The chess player must constantly absorb, filter, sort, process, evaluate and decide on information. In person-to-person chess games, additional information for evaluating the move can be obtained from the opponent’s behaviour: sweating, gestures, nervousness, posture, etc.
The chess game is followed by the collective analysis, in which the decisions previously made in the game are ultimately reviewed and evaluated. During the analysis, the persons involved disclose their thought processes, their approach to move selection and move evaluation. In addition, the language skills are trained to express themselves accurately and comprehensibly, to understand, evaluate and accept the arguments put forward. It is easier to learn from mistakes because typical patterns are recognised more quickly and can therefore be avoided more easily. In collective play and collective analysis, the children acquire skills in teamwork, i.e. listening attentively to others, reflecting on what is said, actively participating in the opinion-forming process, dealing with each other respectfully. During the collective analysis, it happens again and again that moves are proposed to win the game, which obviously turn out to be mistakes, because it was overlooked that the opponent simply wins chess pieces and later does not have to fear the game, the threat, the proposed combination is incorrect. This also happens to experienced chess players. Because these mistakes happen to everyone at some point, no one wants to be treated badly because of them. In this way, the group learns to treat each other with respect.
The fact that chess players have to develop strategies for efficient information processing and pattern recognition is made clear by the following facts: In the initial position, White has to decide between 20 possible moves (16 pawn moves and 4 knight moves). After White’s first move, Black also has 20 possible moves (16 pawn moves and 4 knight moves) at his disposal, because his pieces are still in the initial position. There are 20 x 20 = 400 different chess positions after two moves (first move for White, followed by the first move for Black). There are 5,362 different chess positions after three moves (White’s second move). There are 71,852 different chess positions after four moves (two moves for White and two moves for Black). After 5 moves there are already 809,896 different positions and after 6 moves (three moves for White and three moves for Black) there are already 9,132,484 different positions.
Attention spans in children have declined rapidly in recent years as a result of intensive smartphone and internet use. “Just the spatial presence of our own smartphone – with all its fantastic options for distraction – leads to a weakening of our cognitive performance.”[61] Children learn to focus on what is happening on the chessboard when they play chess. One reason can be seen as the competitive nature of chess, because children want to get better. Another reason is the experience of success, i.e., I am attentive in chess lessons, then I make fewer mistakes in my own game and win more games. “Attention is an important personal resource in today’s information society and is crucial for personal performance, motivation and problem-solving ability at all ages.”[62] The competitive character of chess arouses in the children the ambition to become better than the others, i.e. they are motivated to learn.
Research on the influence of chess lessons on mathematics has found a positive correlation with arithmetic. The chess-playing children learn that the pieces have different values and that one minor piece (knight or bishop) corresponds to the value of three pawns. The children learn basic arithmetic and typical mathematical facts such as substitution, ratio and equivalent in the figurative chess environment. The children quickly understand that a rook is equivalent in value to two minor pieces, and that a minor piece with three pawns is equivalent to a rook, at least mathematically.
Examples of calculations with chess pieces:
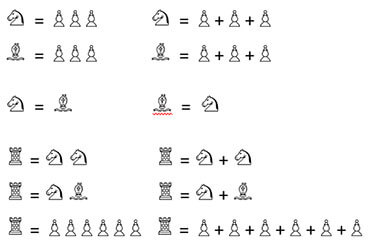
The thought process for the quantitative evaluation of the figures on the chessboard prepares the children for calculating with variables and solving tasks with several unknowns, because the children have already gained their first experience with these patterns and ways of thinking through the game of chess.
When the children start learning chess, the chess board and the orientation on it are first explained in detail. They learn that each square has a name consisting of a letter from A to H and a number from 1 to 8, which are the coordinates of the chessboard. And this form of identifying squares and orientation on the chess board makes it easier to read maps, diagrams and curves. There are probably fewer and fewer children who have already held a city map or a map in their hands. The convenient navigation device in the car or mobile phone has replaced the map. In the navigation device, you enter the place you are looking for and a circle flashes on the screen.
6.1. CHESS PLAYERS THINK IN IMAGES
The chess player has to process a vast volume of visual information on the chessboard and derive from it his concrete action to execute the next move. It is necessary to recognise whether a piece can be captured and whether one receives a countervalue for it, which concrete threats are present or the opponent is planning and to what extent these collide with one’s own plans. And finally, he must choose the best move in the situation, decide to make the one move. To do this, he must run through possible sequences of moves in his mind’s eye and evaluate the resulting chess positions. Different movement patterns of the player’s own and the opponent’s pieces have to be taken into account and combined. For evaluation, experienced chess players refer to experiences and known positional patterns that are stored in the brain.

Chessmen „Flamenco“, made of horseshoe nails, screw parts and forks
Tactics training, i.e. solving chess problems such as “mate in one move” or “mate in two moves” or “white on the move wins” trains seeing. The brain memorises positional patterns and the corresponding winning procedures. The more tactical exercises are solved, the sooner the player is able to recognise underlying patterns (fork, double attack, weak basic line, …), abstract them and apply them in his own games. The position created on the chessboard is compared with the winning positions and winning patterns stored in the brain in order to assess whether, for example, the prerequisites for a successful mating attack are present and whether the known winning method can be applied directly or in a modified form. The transformation of positions, such as the transition from the middlegame to an easily won endgame, is based on a deeper understanding of the chess position. In the end, chess is always about pattern recognition. Experience shows that, for example, free lines, passed pawns, protected passed pawns, space advantage are good prerequisites for the successful chess game. When deciding on the next move, the player must develop plans in his mind’s eye, i.e. desired chess positions, which he wants to achieve. To do this, he must examine different move sequences, i.e. coordinate and evaluate different patterns of movement of the pieces, both his own and his opponent’s, over time.
6.2. CHESS ENCOURAGES CREATIVE PROBLEM SOLVING
The saying “All roads lead to Rome” is also relevant in the natural sciences and in chess. The chess positions that arise in the course of the game can often also be achieved with a different sequence of chess moves.
Example (see chess diagram):
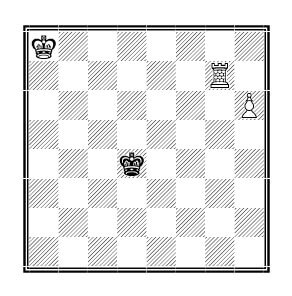
Instead of mating the opponent’s king in an endgame (king, rook and pawn against king) with the united forces of king and rook, the pawn can first be promoted to another piece and both pieces together mate the opponent’s king.
In principle it is obvious that it is easier to mate with queen and rook together. Nevertheless, it is not a guarantee for victory. Beginners in particular overlook the stalemate motif, i.e. the opponent’s king is not in check and also has no possibility of making a legal move. In a stalemate, the game ends in a draw, the stronger party has given away half a point to the opponent. In order not to run into a stalemate trap, each move must be conscientiously checked before execution, i.e. the situation on the chessboard is analysed in order to recognise stalemate possibilities in time and to avoid them. In the above example, recognising the pattern “staircase mate” leads to quick success. If the winning staircase mate is implemented consistently, there is also no danger of the black player being “given” half a point because of a stalemate. In time pressure phases of the game of chess, supposedly complicated ways of winning can be useful, because the player executes the moves routinely and thus without losing time for additional considerations and controls.
And this experience of choosing from several solutions that lead to the goal is often enough prevented in school lessons. There are mathematics teachers who only recognise one solution as correct, and that is the one they have explained in class. In this case, pupils are slowed down, creativity is restricted and disinterest spreads. The method presented by the teacher to solve the task does not have to be the quickest, easiest or most understandable method for the pupil. It is remembered that there are countless calculation methods for adding or multiplying multi-digit numbers together.[63]
Offering and allowing different ways of calculating to solve the problems in mathematics and in the other sciences invites the pupils to participate and reflect. Is the rule of three really a simple and understandable calculation method? Or is another calculation method such as the relation equation with representation in fraction notation more universal, simpler and easier to understand? Which method is more suitable for mental arithmetic? (cf. Appendix B)
It can be observed among chess beginners that wishful thinking prevails at first. They hope that their opponent will make the obviously worst move, which will lead to the loss of the game. This hoping for the lucky circumstance that the opponent makes a blunder is replaced, with increasing playing experience, by the realisation that one’s own move selection is more successful based on analytical considerations. There is an increasing conscious search for the best moves for both sides. In other words, you have to be honest with yourself and think self-critically if you want to win the chess game. Intuitively, the player familiarises himself with the dialectical principle of “cause and effect” when he mentally goes through the possible moves and weighs up which move could bring him the greatest benefit. The insights just described help the children to better grasp the above-mentioned task on probability calculation (different coloured balls in a box) and to find the correct solution independently.
In addition to self-critical thinking, the children learn to take responsibility. No matter how the game ends, the player is responsible for success or failure. There are no excuses like:
- the opponent had an advantage because of tailwind support,
- the ground was muddy
- had no chance to intervene (in football or handball: because the ball was not passed to him)
- because the opponent fouled him
The children who learn chess experience that attention and additional occupation with chess lead to more winning games. They are rewarded for their diligence with a sense of achievement. This strengthens their self-confidence in their own abilities and leads to positive changes in their attitude towards learning. Chess promotes motivation to learn.
Experienced chess trainers know that games replayed on the real chess board are better remembered than games replayed on the computer. One’s own activity – moving the chess piece on the chessboard – is a complex process, comparable to that of writing, if one looks closely enough.
Besides classical chess, there are many other types of chess that are fun for children – such as losing chess or tandem chess. In tandem chess, two teams consisting of 2 players play on 2 chess boards. The two players of a team play with opposite colours. Each player plays at his board against a direct board opponent. The special feature is that the captured piece is passed on to the team partner, who may then use it on the chessboard according to previously agreed rules. A team has won when a player has checkmated the opponent on his board. To be successful, the players in the team must negotiate and implement a common strategy. The chosen strategy must be regularly adapted to the actual play on the two chess boards, i.e. one must react flexibly, compromise with oneself and one’s partner and act harmoniously as a team. Time becomes an additional dimension, because a wait-and-see approach to a game means not providing the opposing team with pieces from an exchange (capturing pieces) that can then be used to attack or defend.
Even if not all the effects of chess on personality traits and learning success have been described and mentioned here, this presentation helps to sense and grasp what a powerful learning-didactic instrument chess is.
With this knowledge, it is easier to understand why more chess-playing children than non-chess-playing children are interested in STEM professions.[64] A selection of scientific research on the effects of chess instruction on mathematics, German language and various personality traits is given in Appendix A.
The brochure “Chess – a tool for education and health” (Link) mentions even more effects of chess on personality development. The brochure is available in several languages.
There are countless ideas and scientific papers on how chess can be used in the classroom and in various subjects outside the mathematics lesson. An overview can be found on the internet Link.
As can be read again and again in the papers, the game of chess gives children a lot of pleasure. Chess is not only serious, but also cheerful. Since time immemorial, there have been artists, poets and writers who have dealt with chess. Humorous poems, novels, films, comics, cartoons and pictures were created.
7. WITH THE LEARNING-DIDACTIC GAME “CHESS” COST-EFFICIENTLY TO MORE LEARNING SUCCESS IN SCHOOL
Chess is an inexpensive and effective resource for activating mental activity. Providing schools with chess sets is not very expensive. If the chess boards and chess pieces are handled carefully, there is no need to replace them for a long time. Large-field chess in the schoolyard offers a meaningful activity during the breaks, promotes communication between the pupils and provides relaxation. Teachers and after-school educators report that chess reduces aggressive behaviour.
The positive impact of chess on school performance brings benefits to society. The monetary value was first calculated in Denmark in 2021. “DAMVAD Analytics”, a Danish consultancy for advanced analytics and artificial intelligence calculated an economic benefit of about 134 million euros in five years , if all children have regular chess lessons.[65] The socio-economic gain results from the positive effects of chess on personality development and learning success described above. Better performance in mathematics education is associated with fewer school drop-outs, less delinquency, better job perspectives and, as a consequence, higher income. Saved expenditure in the health sector is more difficult to quantify.
The development and use of learning tools was not included in the analysis. How economical is it to develop individual tools (learning-didactic games, workbooks, therapies, …) for the many known learning problems? Such useful tools, which are often developed for specific learning problems, should meet the following requirements:
- simple enough to be able to use the tools without setting up new hurdles,
- readily available so that they can be used anywhere,
- easy to use so that different people can work with it. (Not only trained professionals, but also parents, children, coaches can take on the role of therapist).
- great chances of success in achieving the intended learning goals (which would first have to be proven in extensive studies for each aid, analogous to new medical products)
- The assistive tool should not stigmatise the learner because he or she receives “special treatment” by means of special assistive tools. This can have a negative impact on self-image, motivation and learning outcomes, apart from possible psychological problems because the learner feels “labelled”, perhaps as an inferior person.
- The use of the tools is enjoyable because it has a positive effect on the motivation to use the tool repeatedly and independently.
- Inexpensive, in order to be able to help many
In summary, it can be said: Chess is not a miracle formula that will solve all problems. Rather, chess is a powerful, universally effective learning-didactic tool, which can produce amazing results for broad groups of students. Educators do not have to be excellent chess players to use chess in the classroom. The playful element of chess is in the foreground. The teachers guide the children through the chess lesson. There is a vast amount of chess literature available worldwide that can be used directly in lesson planning and implementation. Chess programmes can also be used. They explain the rules of chess in a clear and child-friendly way and offer entertaining exercises. The children can learn chess independently at their own pace. In every lesson, the children should play chess with each other. They can try out and apply what they have learned. It is important that the children look forward to the chess lesson. Then, over time, positive effects will emerge, which scientists have proven in many studies.
The case for including chess among school curricula is usually based on the benefits for improving math skills. But this is not the only benefit of chess. Chess is a prime example of an interdisciplinary activity. Teaching chess in German schools would train children to see the unity of all the other disciplines they learn at school. It would challenge them to use their minds, and yes, even their bodies, to learn, compete and have fun. (based on Prof. Michael Hickson, University of Trent, Kanada)[66]
Further information on https://www.chess-science.com
In English:
- Jerry Nash: “Chess can improve the student-teacher dynamic” – Link to chessbase (English)
In German:
- Schach – die Schatzkiste der Bildungspolitiker (Chess – the treasure box of education politicians) (update zum Beitrag vom 05.02.2022) – Link
- Schulschach ist eine enorme sozioökonomische Ressource mit immensen finanziellen Vorteil für die Gesellschaft (School chess is an enormous socio-economic resource with immense financial benefits for society) (05.02.2022) – Link
- Zusammenhang zwischen Arbeitsgedächtnis, Lernerfolg und Schach – der Weg zu mehr Lernerfolg (Connection between working memory, learning success and chess – the way to more learning success) – Link
- Möglichkeiten, Schach in der Arbeit des pädagogischen Psychologen im Bereich der Bildung einzusetzen (Possibilities to use chess in the work of the educational psychologist in the field of education) – Link
- Lesenswerte Details zu Antworten auf den Brandbrief 2017, der Mathematikdefizite von Studienanfängern beklagte (mit Aufgabenbeispielen, 2018) (Worth reading details of responses to the 2017 urgent letter complaining about mathematics deficits of first-year students (with examples of tasks, 2018))– Link
REFERENCES
[1] Benjamin Franklin (1706 – 1790) – American writer, scientist and statesman
[2] Kollosche, D. (2018). Soziale Dimensionen der Wahrnehmung von Mathematik durch Schüler. In: Nickel, G., Helmerich, M., Krömer, R., Lengnink, K., Rathgeb, M. (eds) Mathematik und Gesellschaft. Springer Spektrum, Wiesbaden. https://doi.org/10.1007/978-3-658-16123-1_22
[3] IQB-Bildungstrends 2021, Seite 54
[4] IQB-Bildungstrends 2021, Seite 55
[5] 17.10.2022 „KMK stellt sich neuesten Befunden des IQB-Bildungstrends: Gezielte Maßnahmen zur Sicherung der Mindeststandards sind notwendig“, URL: https://www.kmk.org/aktuelles/artikelansicht/kmk-stellt-sich-neuesten-befunden-des-iqb-bildungstrends-gezielte-massnahmen-zur-sicherung-der-minde.html
[7] Nationaler PISA-Bericht 2018, Seite 204 ff.
[8] Spiegel online, Zahl der Schulabgänger ohne Abschluss steigt (Number of school leavers without qualifications increases) (2020) URL: https://www.spiegel.de/panorama/bildung/bildungsbericht-des-bundes-zahl-der-schulabgaenger-ohne-abschluss-steigt-a-d856b93b-f851-4266-be73-22982af83dfe
[9] 2019, Bildungsstandards im Schulfach Mathematik, Brief an die die Kultusministerkonferenz https://angewandte-didaktik.mathematik.uni-mainz.de/files/2020/03/Brief-KMK-20190815-Bildungsstandards.pdf
[10] Hafner, T. (2012). Proportionalität und Prozentrechnung in der Sekundarstufe I. Empirische Untersuchung und didaktische Analysen (Dissertation). Wiesbaden: Vieweg+Teubner
[11] Gudladt, P. (2021). Didaktische Überlegungen. In: Inhaltliche Zugänge zu Anteilsvergleichen im Kontext des Prozentbegriffs. Perspektiven der Mathematikdidaktik. Springer Spektrum, Wiesbaden. https://doi.org/10.1007/978-3-658-32447-6_2
[12] Die Gartenlaube (1890). Ernst Keil’s Nachfolger, Leipzig 1890, Seite 548. Digitale Volltext-Ausgabe bei Wikisource, URL: https://de.wikisource.org/w/index.php?title=Seite:Die_Gartenlaube_(1890)_548.jpg&oldid= – (Version vom 20.1.2023)
[13] Spektrum der Wissenschaft, 10.10.2013, Rechenschwäche gibt es nicht, URL: https://www.spektrum.de/news/rechenschwaeche-gibt-es-nicht/1209908
[14] Gaidoschik, Michael & Moser Opitz, Elisabeth & Nührenbörger, Marcus & Rathgeb-Schnierer, Elisabeth & Götze, Daniela. (2021). Besondere Schwierigkeiten beim Mathematiklernen. 10.13140/RG.2.2.15952.64004., URL: https://www.zebis.ch/unterrichtsmaterial/besondere-schwierigkeiten-beim-mathematiklernen
[15] Gaidoschik, Michael & Moser Opitz, Elisabeth & Nührenbörger, Marcus & Rathgeb-Schnierer, Elisabeth & Götze, Daniela. (2021). Besondere Schwierigkeiten beim Mathematiklernen. 10.13140/RG.2.2.15952.64004., URL: https://www.zebis.ch/unterrichtsmaterial/besondere-schwierigkeiten-beim-mathematiklernen
[16] Psychologie für den Lehrberuf Urhahne, D., Dresel, M., Fischer, F. 2019, XVI, 636 S. Mit Online-Extras, Hardcover ISBN: 978-3-662-55753-2, 28, URL: https://lehrbuch-psychologie.springer.com/sites/default/files/atoms/files/urhahne_a1_978-3-662-55753-2_leseprobe_1.pdf
[17] Viesel-Nordmeyer, N., Ritterfeld, U. & Bos, W. Welche Entwicklungszusammenhänge zwischen Sprache, Mathematik und Arbeitsgedächtnis modulieren den Einfluss sprachlicher Kompetenzen auf mathematisches Lernen im (Vor‑)Schulalter?. J Math Didakt 41, 125–155 (2020). https://doi.org/10.1007/s13138-020-00165-0
[18] The terms „power“ and „labor productivity“ are described in German with the one word “Leistung”
[19] Stegariu, Vlad-Ionut, and Beatrice Abalasei. “Correlation between Attentional Abilities and Spatial Orientation in Children Who Study Chess in School.” Revista Romaneasca pentru Educatie Multidimensionala 14.3 (2022): 126-138. URL: https://www.lumenpublishing.com/journals/index.php/rrem/article/download/5267/3910
[20] Winkelmann, Jan, Mareike Freese, and Tim Strömmer. “Schwierigkeitserzeugende Merkmale im Physikunterricht: Die Perspektive von Schüler* innen.” Progress in Science Education (PriSE) 5.2 (2022): 6-23. URL: https://e-publishing.cern.ch/index.php/prise/article/download/1168/1112/5559
[21] Richard Feynman (1918-1988) – American physicist and Nobel Prize winner
[22] Lin-Siegler, X., Ahn, J. N., Chen, J., Fang, F. F. A., & Luna-Lucero, M. (2016). Even Einstein struggled: Effects of learning about great scientists’ struggles on high school students’ motivation to learn science. Journal of Educational Psychology, 108(3), 314, URL: https://psycnet.apa.org/manuscript/2016-07217-001.pdf
[23] Siehe Fußnote 18 (Lin-Sigler)
[24] SWR2, 28.10.2022 , URL: https://www.swr.de/swr2/wissen/problemfach-mathe-wie-schule-fuer-zahlen-und-logik-begeistern-koennte-swr2-wissen-2022-10-29-100.html
[25] IQB-Bildungstrends 2018, Seite 372
[26] IQB-Bildungstrends 2018, Seite 447
[27] Fischer, Marc; Irgl, Christian. ” Mit den Tiefenstrukturen wird der Blick stärker auf die Schüler*innen und auf ihre Lernprozesse gerichtet.” Das Heft-Pädagogische Hochschule FHNW. (2020) 4. URL: Link
[28] Yu, Qinmei, Stella Patino, and Tracy Harris. “Creating Joyful “Third Space” for Young Dual Language Learners via Family-involved Chess Playing Project.” Journal of Education and Human Development 9.4 (2020): 108-116.
URL: http://jehdnet.com/journals/jehd/Vol_9_No_4_December_2020/11.pdf
[29] Lynn Arthur Steen (1941 – 2015) – American mathematician and mathematics teacher
[30] Koerber, S., Mayer, D., Osterhaus, C., Schwippert, K. and Sodian, B. (2015), The Development of Scientific Thinking in Elementary School: A Comprehensive Inventory. Child Dev, 86: 327-336. https://doi.org/10.1111/cdev.12298
[31] Steen, Lynn Arthur. “Reflections on Mathematical Patterns, Relationships, and Functions.” Prepared for the Minnesota K-12 Mathematics Framework, SciMath-MN (1998). URL: http://www.steen-frost.org/Steen/Papers/98algebra_mn.pdf
[32] Ch, Erich & Wittmann,. (2005). Mathematics as the science of patterns–a guideline for developing mathematics education from early childhood to adulthood. Link
[33] Vogel, R. Muster – eine Grundidee des mathematischen Denkens und Lernens. ZDM 37 , 445–449 (2005). https://doi.org/10.1007/s11858-005-0035-z
[34] Maries, Alexandru, and Chandralekha Singh. “Helping Students Become Proficient Problem Solvers Part I: A Brief Review.” Education Sciences 13.2 (2023): 156., URL: https://www.mdpi.com/2227-7102/13/2/156
[35] Bilalić, Merim, et al. “Mechanisms and neural basis of object and pattern recognition: a study with chess experts.” Journal of Experimental Psychology: General 139.4 (2010): 728. URL: https://cognition.aau.at/download/Publikationen/Bilalic/Bilalic_etal_2010a.pdf
[36] John F. Kennedy (1917 – 1963) – 35th president of the United States
[37] Spitzer, Manfred. “Keilschrift, Kant und Kaufverträge.” Nervenheilkunde 39.04 (2020): 198-205. URL: https://www.thieme-connect.com/products/ejournals/html/10.1055/a-1033-9748
[38] Buddeberg, Magdalena, and Anke Hußmann. “Kapitel I Verlängerte Unterrichtsstunden aus Sicht von Lehrkräften sowie Schülerinnen und Schülern.” Mareike Haas und Maria Krieg (Hg.) (2021): 15-28. URL: Link
[39] Haunhorst, D., Hüfner, C., Kastrup, V., Mergelkuhl, T., Röllke, K., & Wilde, M. (2022). Sport und Biologie fächerübergreifend unterrichten : Die Planung und Umsetzung fächerübergreifender Unterrichtskonzepte im Rahmen eines universitär begleiteten Schulpraktikums. Herausforderung Lehrer*innenbildung – Zeitschrift Zur Konzeption, Gestaltung Und Diskussion, 5(1), 26–42. https://doi.org/10.11576/hlz-5152
[40] Kramer, N., & Wegner, C. (2020). Fächerübergreifender Unterricht im Fächerverbund Naturwissenschaften und Sport: Darstellung eines systematischen Reviews. Herausforderung Lehrer*innenbildung – Zeitschrift Zur Konzeption, Gestaltung Und Diskussion, 3(1), 689–715. https://doi.org/10.4119/hlz-2544
[41] Blanch, A. Chess Instruction Improves Cognitive Abilities and Academic Performance: Real Effects or Wishful Thinking?. Educ Psychol Rev 34, 1371–1398 (2022). https://doi.org/10.1007/s10648-022-09670-9
[42] Blanch, A. Chess Instruction Improves Cognitive Abilities and Academic Performance: Real Effects or Wishful Thinking?. Educ Psychol Rev 34, 1371–1398 (2022). https://doi.org/10.1007/s10648-022-09670-9
[43] siehe Fußnote 36
[44] Tyler W. Watts, Drew H. Bailey & Chen Li (2019) Aiming Further: Addressing the Need for High-Quality Longitudinal Research in Education, Journal of Research on Educational Effectiveness, 12:4, 648-658, https://doi.org/10.1080/19345747.2019.1644692
[45] Direkter Link zur Tabelle URL: https://link.springer.com/article/10.1007/s10648-022-09670-9/tables/2
[46] Zaretskiy V. K., CHESS FOR GENERAL DEVELOPMENT: REFLECTIVE AND ACTIVITY APPROACH TO CORRECTING BEHAVIORAL DISORDERS (2018), URL: https://www.mental-health-congress.ru/media/document/final_document/29/СБОРНИК%20НАУЧНЫХ%20СТАТЕЙ.pdf
[47] Lev Vygotsky(1896 – 1934) Soviet psychologist, In Russian: „Один шаг в обучении может означать сто шагов в развитии.“
[48] Zaretskiy V. K., Glukhova O. V. ” The reflexive activity approach to teaching chess at school: Satka experience” II International Conference on Consultative Psychology and Psychotherapy dedicated to the memory of F.E. Vasilyuk: collection, no. 1, 2020, pp. 100-104. https://doi.org/10.24411/9999-055A-2020-00023
[49] in Russian „способность действовать в уме“, more information: Zak A.Z. CHARACTERISTICS OF THE ABILITY TO ACT “IN THE MIND” OF FIRST-GRADERS // Международный журнал гуманитарных и естественных наук. 2022. №10-2. URL: https://cyberleninka.ru/article/n/characteristics-of-the-ability-to-act-in-the-mind-of-first-graders
[50] Barma, S. & Zaretskii, Z. K. (2017), Contemporary Russian Contributions to Vygotsky’s Heritage. Special Issue. CRI_SAS International Journal/Revue internationale du CRIRES: innover dans la tradition de Vygotsky, 4(1). ISSN:2291–6717, URL: https://revues.ulaval.ca/ojs/index.php/RIC/issue/view/22
[51] Glukhova O.V., Volikova S.V., Zaretsky Y.V., Zaretsky V.K. The Results of a Longitudinal Diagnostic Study on the Project «Chess for Overall Development». Konsul’tativnaya psikhologiya i psikhoterapiya = Counseling Psychology and Psychotherapy, 2022. Vol. 30, no. 4, pp. 49–75. URL: https://doi.org/10.17759/cpp.2022300404 . (In Russ., аbstr. in Engl.)
[52] Romanova, I., Vasylieva M., Podberezskyi.M. “Chess therapy as a new trend in training of future social pedagogues.” (2018). URL: http://efsupit.ro/images/stories/october2018/Art%20266.pdf
[53] Panagiotidi, M., Overton, P. Aufmerksamkeitsdefizit-Hyperaktivitätssymptome sagen eine problematische Mobiltelefonnutzung voraus. Curr Psychol 41 , 2765–2771 (2022). https://doi.org/10.1007/s12144-020-00785-2
[54] Veloso A, Vicente SG and Filipe MG (2020) Effectiveness of Cognitive Training for School-Aged Children and Adolescents With Attention Deficit/Hyperactivity Disorder: A Systematic Review. Front. Psychol. 10:2983. URL: https://doi.org/10.3389/fpsyg.2019.02983
[55] Yanguas, María Rodrigo. Efectividad de una aplicación informática personalizada basada en el ajedrez para el tratamiento de niños y adolescentes con trastorno de déficit de atención con hiperactividad (TDAH): Un ensayo clínico. Diss. Universidad Autónoma de Madrid, 2021.
[56] Scholz, Markus, et al. “Impact of Chess Training on Mathematics Performance and Concentration Ability of Children with Learning Disabilities.” International Journal of Special Education 23.3 (2008): 138-148. URL: https://files.eric.ed.gov/fulltext/EJ833690.pdf
[57] URL: https://www.zeit.de/2022/33/jarno-scheffner-schach-amateur-weltmeister
[58] Sidorenko A.A. Teaching Chess on the Basis of the Refletiive-Activity Approach in the Context of the Problem of Gaining Legal Capacity: a Case from Practice. Konsul’tativnaya psikhologiya i psikhoterapiya = Counseling Psychology and Psychotherapy, 2022. Vol. 30, no. 4, pp. 76–96. https://doi.org/10.17759/cpp.2022300405 (In Russ., аbstr. in Engl.)
[59] AlphaZero is a autodidactic computer program by DeepMind, whose algorithm learns several complex board games using only the rules of the game and winning conditions, and by playing intensively against itself. (German Wikipedia)
[60] Franklin, James. “Mathematics as a science of non-abstract reality: Aristotelian realist philosophies of mathematics.” Foundations of Science 27.2 (2022): 327-344, URL: https://philpapers.org/archive/FRAMAA-12.pdf
[61] Kreutzer, R.T. (2020). Mangelnde Konzentrationsfähigkeit. In: Die digitale Verführung. Springer, Wiesbaden. https://doi.org/10.1007/978-3-658-27781-9_2
[62] John, D.T., Wieland, U., Blickhan, D. (2019). Achtsamkeitsinterventionen in der Schule. In: Chang-Gusko, YS., Heße-Husain, J., Cassens, M., Meßtorff, C. (eds) Achtsamkeit in Arbeitswelten. FOM-Edition. Springer Gabler, Wiesbaden. https://doi.org/10.1007/978-3-658-25673-9_11
[63] Vgl. Miller, Maximilian „Rechenvorteile“( Calculation advantages). BSB B.G. Teubner Verlagsgesellschaft Leipzig. (1963)
[64] Zlabinger, Florian. Mathematik und Schach: Ansichten schachspielender Kinder und Jugendlicher zum Themengebiet Mathematik/eingereicht von Florian Zlabinger, BSc. Diss. Universität Linz, 2021. URL: https://epub.jku.at/obvulihs/content/titleinfo/5884149/full.pdf
[65] „En times skoleskak om ugen giver en stor samfundsøkonomisk gevinst“, https://www.danskindustri.dk/lad-os-lose-det-sammen/cases/cases/damvad-analytics-x-dansk-skoleskak/ (December 2021)
[66] Michael Hickson, „Why Canada should invest more in teaching kids how to play chess“. The Conversation. (13.10.2022) URL: https://theconversation.com/why-canada-should-invest-more-in-teaching-kids-how-to-play-chess-191413
APPENDIX A OVERVIEW OF SCIENTIFIC PAPERS ON CHESS IN SCHOOLS
Tables based on: Ortiz-Pulido, Ricardo, et al. “Neuroscientific evidence support that chess improves academic performance in school.” Revista mexicana de neurociencia 20.4 (2019): 194-199.
URL: https://www.medigraphic.com/pdfs/revmexneu/rmn-2019/rmn194e.pdf
Table 1
Some studies that have found that chess influences mathematical achievement at school
| Author(s) | Country | Number of
participants |
Study objective | Tests | Results |
| Fernandez-Amigo et al.
T1 (Year 2008) |
Spain | N = 141 experimental
group (79 boys, 62 girls) |
Analyze, qualitatively and
quantitatively, the utility of instructional materials using chess for teaching mathematics during the second grade of primary school. |
EFAI (Factorial
Evaluation of Intellectual Aptitudes) Numerical score, reasoning score, ethnographic interview, surveys |
Satisfaction was
achieved in the utility of the chess ‑ based learning materials for teaching mathematics |
| Achig and Francisco
T2 (Year 2015) |
Ecuador | N = 35 experimental group (20 boys, 15 girls) | Test the impact of chess
on logical‑mathematical reasoning in sixth‑grade primary school students |
Theoretical chess test
before and after, Mathematics class score |
The average math
class score increased |
| Guerrero et al.
T3 (Year 2015) |
Mexico | N = 32 The number
of boys versus girls is not given. |
Describe the effect of
chess on basic mathematical operations in fifth‑grade primary school students |
Pre‑intervention tests,
characteristics of the child and the child’s mother and father |
Better concentration,
and memory and higher math class score |
| Gumede and Rosholm
T4 (Year 2015) |
Danmark | N = 264 The number
of boys versus girls is not given |
Characterize the impact of
chess in the subject of mathematics in first‑and third‑grade primary school students |
Pre-intervention tests, personal characteristics of the child and of the child’s mother and father. | Positive effects in
both immigrant and non‑immigrant Danish children |
| Sala et al
T5 (Year 2015) |
Italy | N = 309 experimental group
(169 boys, 140 girls) N = 251 control group (116 boys, 135 girls) |
Investigate the potential
of online chess lessons on problem‑solving abilities in second, fourth, and fifth‑grade primary school students |
Programme for
International Student Assessment (PISA) and chess survey |
Highly positive correlation between math
score and chess in the experimental group |
| Sala et al
T6 (Year 2016) |
Italy | N = 309 experimental group
(169 boys, 140 girls) N = 251 control group (116 boys, 135 girls) |
Experimental study of
chess in fourth grade primary school students using a placebo group |
Six tests evaluating
mathematics abilities, IEA – TIMSS psychometric test |
The chess group was more effective in math skills than the GO group, but not in school activities |
| Rosholm et al.
T7 (Year 2017) |
Danmark | N = 323 Test group.
N = 159 Control group |
Analyze the effect of replacing one mathematics lesson per
week with one based on chess instruction in first and third grade primary school students |
Mathematics test (including calculations, geometry, pattern recognition, and basic problem solving) | Improvement in the composition of mathematical sequences in the experimental group |
| Meloni and Fanari
T8 (Year 2019) |
Italy | N = 48 experimental group.
N = 37 Control group |
Analysis of the effects of replacing one maths lesson per week with a chess lesson for primary school pupils in the first and third grades | Mathematics test (including calculations, geometry, pattern recognition and basic problem solving) | Improving the formation of mathematical sequences in the experimental group |
| Tachie and Ramathe
T9 (Year 2022) |
South Africa | N = 25
experimental group N = 26 Control group The number of boys versus girls is not given. |
Analysis of the effects of replacing one mathematics lesson per week with a chess lesson for ninth grade students | Group test | The chess group was more effective in mathematical skills |
Table 2
Some papers investigating the influence of chess on reading comprehension in school
| Author(s) | Country | Number of
participants |
Study objective | Tests | Results |
| Margulies et al
T10 (Year 1991) |
USA | N = 1118, groups of participants N = 22 | Escribe the effect on
reading before and after chess instruction in primary school |
Degree of reading
power test (DRP) |
The group of chess students
improved more than the average student. |
| Liptrap et al
T11 (Year 1998) |
USA | N = 67 Group
that did not play chess N = 504 |
Determine the degree of participation by students in a chess club | Texas Assessment of Academic Skills (TAAS). Texas Learning Index (TLI) | The chess group improved
more in math skills than in reading |
| Duccette
T12 (Year 2009) |
USA | Experimental
group N = 151 |
Analyze the effect of a chess program on behavior, math, and reading | Philadelphia’s behavior grade and attendance, Pennsylvania System of school Achievement (PSSA)
Score in reading and mathematics |
After 1 year, the group that played chess improved in math and reading, and these values were correlated, while
in the control group none of these patterns were present. |
| Dapica Tejada
T13 (Year 2016) |
Spain | N = 60 Total
Chess group N = 30 (21 boys, 9 girls) Control group N = 30 (20 boys, 10 girls) |
Test whether there
are significant differences in reading comprehension and saccadic movements (SM*) in boys and girls that play chess. |
Chess participation
survey, PROLEC‑SE battery of tests of reading processes and the King Devick SM test |
The chess group improved on the different tests by which they were evaluated, which did not occur in the no‑chess group. In addition, there was a correlation between SM and reading comprehension
and between chess and SM |
| Celiz
T14 (Year 2020) |
Peru | N = 56 Total
Chess group N = 27 Control group N = 27 |
The effect of chess on the reading comprehension of primary school pupils in the third grade | Pre-test and Post-test | Reading comprehension
improved |
*SM are produced in the eyes when we read, look, or search for information, refers to movement speeds of 500º/S. During these MS, the eyes can remain still for intervals of around 200‑300 ms.
Table3
Some papers investigating the influence of chess on personality traits
| Author(s) | Country | Number of
participants |
Study objective | Tests | Results |
| Filipp et al
T15 (Year 2007) |
Germany | N = 84
Chess group N = 83 Control group |
Impact of chess on mental and academic development in first to fourth grade students, over 3 years. | Basic Intelligence Test Scale Differential Performance Test
Ability to Concentrate (TPK) Hamburg Writing Test Questionnaire |
The chess group performed above average in reading comprehension, arithmetic, Improvements in attitudes and social behaviour |
| Aciego et al.
T16 (Year 2012) |
Spain | N = 170
Chess group
N = 60 Control group |
Effects of regular chess lessons on intellectual and socio-affective abilities | Performance test WISC-R
Self-assessment TAMAI Pretest and posttest External evaluation |
The chess group improved in cognitive and socio-affective skills (self-confidence, motivation to learn, attention, visuo-motor coordination,…). |
| Ramos et al
T17 (Year 2017) |
Argentina | N = 65 Total
(42 boys, 23 girls) Chess group N = 30 (28 boys, 2 girls) Control group N = 35 (14 boys, 21 girls) |
Analysis of the differences in cognitive performance between children who practise chess and children who do not practise chess | Ex post facto cross-sectional study
Stroop Word Colour Test WISC IV WCST Labyrinth test according to Porteus Multivariate variance analysis |
The chess group achieves higher scores in planning, working memory, cognitive flexibility |
| Joseph et al.
T18 (Year 2018) |
India | Chess group
N = 70 (43 boys, 27 girls) Control group N = 81 (52 boys, 29 girls) |
Effects of systematic chess training on verbal reasoning | Pretest and posttest
ANCOVA Binet-Kamat Intelligence Test |
After 2 years, significant increase in linguistic thinking ability in the chess group, no differences between the sexes |
| Atashafrouz
T19 (Year 2019) |
Iran | N = 40 Total
Chess group N = 20 Control group N = 20 |
Effects of chess on problem-solving ability, working memory and concentration for tenth-grade students | Pretest and Posttest,
Cassidy and Lang’s problem-solving style questionnaire (PSSG), Cornoldi’s working memory test (CWMT) and Weinstein and Palmer’s learning and study strategies inventory (LASSI) |
The chess group showed significantly better results for working memory and concentration. |
| Gündüz et al
T20 (Year 2019) |
Turkey | N = 25 Total
Speer Trainees N = 20 Peer Trainers N = 5 |
Impact of chess teaching as peer learning in primary school classrooms | Questionnaires
Peer Evaluation Forms Surveys |
Improvement of cognitive skills, communication and social behaviour |
| Sandoval-Tipán and Ramos-Galarza
T21 (Year 2020) |
Ecuador | N = 60 Total
(41 boys, 19 girls) Chess group N = 30 Control group N = 30 |
Effects of chess on working memory and planning ability in primary school pupils | ENFEN test battery,
Labyrinth test according to Porteus, observation questionnaire |
The chess group showed significantly better results for working memory and planning ability. |
| Tanajyan et al
T22 (Year 2021) |
Armenia | N = 264 Total
Distribution of pupils by class level, school type and gender |
Attitudes towards chess education and its effects on the social behaviour of children in the second to fourth grade | Standardised Interview with Multiple Choice
Tests – Rokeach theory of values |
The vast majority enjoy playing chess,
Positive effect on cooperation behaviour, motivation, honesty, planning, discipline. |
| Gao et al.
T23 (Year 2021) |
China | N = 255 Total
Distribution of pupils by class level, school type and gender |
Relationships between fluid intelligence, skills in chess and school performance | Raven’s Standard Progressive Matrices
Survey School exams Multivariate variance analysis |
positive correlation between fluid intelligence and school performance,
Chess skills correlate with academic performance. |
| Glukhova
T24 (Year 2022) |
Russia | 1st phase
N = 637 Total Chess group 1 N=331 with chess project” teaching programme Chess group 2 N = 160 with “Chess universal” teaching programme Control group N = 146 without chess programme
across all phases N = 1571 there-of N = 723 with teaching programme “chess project |
Increasing the developmental level of intellectual processes in children by means of chess based on the approach of reflection activity with pupils of the first to ninth grade over 4 years and long-term effect,
18 years in total |
Memory test,
Visual memory test Analogy tests Raven’s Standard Progressive Matrices Correction test Bourdon |
Stable improvement of intellectual performance,
of the chess groups Developmental advantage is maintained into high school grades |
| Chitiyo et al.
T25 (Jahr 2023) |
USA | N = 1286 Total
Distribution of pupils by class level, school type and gender |
To identify differences in students’ perceived benefits of chess by gender and age, as well as by different schools and year groups.
To determine Benefits: Enjoyment, self-confidence, organisational skills, motivation to learn, self-efficacy, ability to cooperate, organisational skills. |
Retrospective pretest and posttest
Multivariate analysis of variance |
Motivation to learn highest among primary school pupils and more among girls than boys in all grades,
Enjoyment was higher among boys than girls, with primary school pupils having the most enjoyment, Cooperativeness improved most among primary school pupils, Perception of benefits depends on gender and grade level. |
to table 1
- Fernández-Amigo J, Gairín Sallán J. Utilización de Material Didáctico con Recursos de Ajedrez Para la Enseñanza de las Matemáticas Barcelona. España: universidad de Barcelona; 2008,
URL: https://www.tesisenred.net/handle/10803/5053
- Achig F, Francisco J. Artículo Científico-Incidencia de la Enseñanza del Ajedrez en la Asignatura de Matemáticas en los y las Estudiantes del 6to. año de Educación Básica de la Unidad Educativa Hermano Miguel de la Salle-Cuenca en el Período de Enero a Junio de 2012-2015, URL: http://repositorio.espe.edu.ec/xmlui/handle/21000/7049
- Guerrero SG, Martínez RM, Alonzo MM. EL ajedrez para el aprendizaje de operaciones básicas y números fraccionarios en un grupo de quinto grado de educación primaria. Rev Invest Educ Esc Grad Educ. 2015;6:9-14. URL: https://sibi.upn.mx/cgi-bin/koha/opac-detail.pl?biblionumber=197301
- Gumede K, Rosholm M. Your Move: the Effect of Chess on Mathematics Test Scores. Discussion Paper; 2015 URL: https://docs.iza.org/dp9370.pdf
- Sala G, Gorini A, Pravettoni G. Mathematical problem-solving abilities and chess: an experimental study on young pupils. SAGE Open. 2015;5:2158244015596050 URL: https://doi.org/10.1177/2158244015596050
- Sala G, Gobet F, Trinchero R, Ventura S. Chess instruction enhance mathematical ability in children? A three group design to control for placebo effects. In: does Chess Instruction Enhance Mathematical Ability in Children? Philadelphia, PA: a Three Group Design to Control for Placebo Effects; 2016 URL: https://livrepository.liverpool.ac.uk/3002154/1/sala_cogsci-2016.pdf
- Rosholm M, Mikkelsen MB, Gumede K. Your move: the effect of chess on mathematics test scores. PLoS One. 2017;12:e0177257 URL: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0177257
- Meloni, Carla, and Rachele Fanari. “Chess Training Effect on Meta-Cognitive Processes and Academic Performance.” International Association for Development of the Information Society; URL: https://doi.org/10.33965/celda2019_201911L048
- Tachie, Simon Adjei, and Johnson Motingoe Ramathe. “Metacognition Application: The Use of Chess as a Strategy to Improve the Teaching and Learning of Mathematics.” Education Research International2022; 2022 URL: https://doi.org/10.1155/2022/6257414
to table 2
- Margulies S. The Effect of Chess on Reading Scores. Report. Vol. 10. New York: the American Chess Foundation; 1991. p. 13-25 URL: https://rknights.org/wp-content/uploads/margulies.pdf
- Liptrap JM. Chess and Standard Test Score. London: chess Life; 1998. p. 41-3 URL: https://saintlouischessclub.org/education/research/chess-and-standard-test-scores
- DuCette J. An Evaluation of the Chess Challenge Program of ASAP/After school Activities Partnerships. Philadelphia, PA: after School Activities Parnerships; 2009. p. 1-13 URL: http://il-chess.org/non_joom/youthpdfs/BradASAPsummary.pdf
- Dapica-Tejada R. Influencia del Ajedrez en la Comprensión Lectora y los Movimientos Sacádicos en Niños Madrid. España: universidad Internacional de la Rioja; 2016 URL: https://reunir.unir.net/handle/123456789/4371
- Mamani Celiz, Edwin. La enseñanza del ajedrez para la comprensión lectora en estudiantes de primaria de la unidad educativa “Kalajawira” de la ciudad de La Paz, gestión 2019. Diss. 2020. URL: https://repositorio.umsa.bo/handle/123456789/24961
to table 3
- Filipp, Sigrun-Heide, and H. Spieles. “Fördert Schachunterricht in der Grundschule die geistige Entwicklung der Kinder.” Abschlussbericht über eine Evaluationsstudie zum Schachunterricht in einer Trierer Grundschule. Trier: ZDiag(2007). URL: https://nsv-online.de/downloads/Endbericht-Abschlusskorrektur13-02-07.pdf
- Aciego, Ramón, Lorena García, and Moisés Betancort. “The benefits of chess for the intellectual and social-emotional enrichment in schoolchildren.” The Spanish journal of psychology2 (2012): 551-559. URL: http://chessedu.org/wp-content/uploads/social-emotional-benefits-1.pdf
- Ramos, Larisa, Vanessa Arán Filippetti, and Gabriela Krumm. “Funciones ejecutivas y práctica de ajedrez: un estudio en niños escolarizados.” Psicogente39 (2018): 25-34. URL: http://www.scielo.org.co/pdf/psico/v21n39/0124-0137-psico-21-39-00025.pdf
- Joseph, Ebenezer, et al. “Enhancing verbal reasoning of school children through chess learning.” International Journal of Scientific Engineering and Science7 (2018): 1-3. URL: http://ijses.com/wp-content/uploads/2018/07/181-IJSES-V2N6.pdf
- Atashafrouz, Askar. “The effectiveness of chess on problem-solving, working memory, and concentration of male high school students.” Iranian Evolutionary and Educational Psychology Journal4 (2019): 249-258. URL: https://doi.org/10.29252/ieepj.1.4.2
- GÜNDÜZ, Nevin, and Ü. N. E. R. Umut. “Application and Evaluation of Peer Education Model in Chess Learning.” The Journal of Eurasia Sport Sciences and Medicine3: 103-115. URL: https://dergipark.org.tr/en/download/article-file/1117499
- Sandoval-Tipán, Luis, and Carlos Ramos-Galarza. “Efectos del ajedrez en el funcionamiento neuropsicológico infantil de la memoria de trabajo y la planificación.” Revista Ecuatoriana de Neurología2 (2020): 46-51. URL: http://scielo.senescyt.gob.ec/scielo.php?script=sci_arttext&pid=S2631-25812020000200046
- TANAJYAN, Kristine, Nelli MELKONYAN, and Sirarpi MOVSISYAN. “Chess as a social value.” Main Issues Of Pedagogy And Psychology1 (2021): 32-37. URL: https://miopap.aspu.am/index.php/miopap/article/download/390/352
- Gao, Qiyang, et al. “Does perceived chess skills mediate the relationship between fluid intelligence and academic performance?.” Journal of Psychology in Africa1 (2021): 56-60. URL: https://www.researchgate.net/profile/Chen-Wei-3/publication/349917758_Does_perceived_chess_skills_mediate_the_relationship_between_fluid_intelligence_and_academic_performance/
- Glukhova, Oksana V. “The Need for Chess in School and Its Role in the Dynamics of Child Development.” Revue internationale du CRIRES: innover dans la tradition de Vygotsky1 (2017): 161-168. URL: https://psyjournals.ru/journals/cpp/archive/2022_n4/Glukhova_et_al
- Chitiyo, George, et al. “Students’ perceived benefits of chess: Differences across age and gender.” Journal of Global Education and Research3 (2023): 214-225. URL: https://digitalcommons.usf.edu/jger/vol7/iss3/2/
Downloads – Article as PDF file, Appendices A to C as PDF files
Article with Appendices A to C as PDF-file: Download
Appendix A OVERVIEW OF SCIENTIFIC PAPERS ON CHESS IN SCHOOLS as PDF-file: Download
Appendix B RATIO EQUATION INSTEAD OF THE RULE OF THREE as PDF-file: Download
Appendix C QUOTES ABOUT CHESS as PDF-file: Download
